Анализ и синтез механизмов сенного пресса, страница 4

Нормальные ускорения вычисляем по формулам:

Отрезки, изображающие векторы этих ускорений, равны:

,                                                    

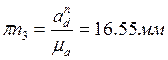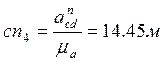
Уравнение (2.40) решаем графически. Проведем линию, параллельную O₁Dиз полюса плана ускорений. Вектор ускорений pn₃направлен к центру O₁. Из точки с проведем параллельно CDотрезок cn₄. Из точки n₃ проведем след ускорения точки D, перпендикулярный O₁D. Из точки n₄  проведем след ускорения точки DвокругC, перпендикулярный CD. На  пересечении получим точку d. Отрезок πd изображает абсолютное ускорение точки D. Отрезок n₄d- тангенциальное ускорение точки DвокругC.

7)  Из плана ускорений находим:

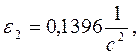
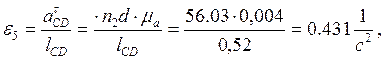
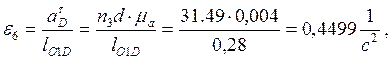
Так как при построении плана ускорений звеньев мы приняли w₁ = const, то

                                  

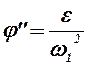
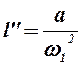
Учитывая, что 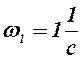, находим

                   

                  

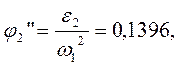
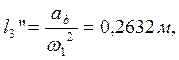
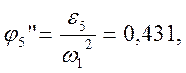
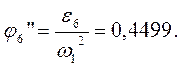
В табл. 2.4 приведены значения аналогов ускорений, полученные графическим и аналитическим методами.

                                                                                                           Таблица 2.4.

Результаты расчета аналогов ускорений.

Величина	j2”	l3”, м	j5”	j6”	S2X”, м	S2Y”, м	S4X”, м	S4Y”, м
Графически	0,1396	0,2632	0,431	0,4499	–	–	–	–
Аналитически	0,1396	0,2632	0,431	0,4499	0,303	-0,129	0,146	-0,113
Отклонение, D %	0,4	2,5	3,3	1,3	–	–	–	–

Аналогично проводим расчет кинематических параметров в остальных положениях механизма.

3. СИЛОВОЙ АНАЛИЗ

3.1. Определение сил инерции

При движении звена различные его точки в общем случае имеют различные ускорения. По принципу Даламбера к каждой точке звена, обладающей элементарной массой dm, следует приложить элементарную силу инерции , где  – ускорение массы dm. Так как звено имеет множество точек, то и сил инерции, действующих на звено, - множество. На практике при расчете самого звена на прочность ограничиваются конечным числом сил инерции, которые сосредоточивают в центрах тяжести. В дальнейшем обычно эти силы приводят к центру масс S звена. В результате на центр масс звена действует результирующая сила инерции (главный вектор инерции), называемая силой инерции , и главный момент сил инерции звена (момент пары сил инерции) .Сила инерции  и момент пары сил инерции . Определяются по формулам соответственно:

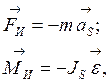
где т – масса звена;  – вектор ускорения масс;  – момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения;  – угловое ускорение звена. Знак минус показывает, что сила и момент и инерции направлены противоположно ускорению.

Находим для исследуемого механизма угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.

Для начального звена в первом положении соответственно будем иметь:

    

Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающим их с аналогами скоростей и ускорений [2, 3], которые имеют следующий вид:

,   

.                                                (5.1)

Результаты расчета ускорений звеньев по формулам (5.1) приведены в табл. 5.1.

Таблица 5.1

Ускорения центров масс и угловые ускорения звеньев

14,735	34,377	8,212	-6,088	24,253	16,992	-6,922	7,441

Определив ускорения звеньев, находим величины моментов и сил инерции звеньев механизма:

- для звена 1      

-для звена 2       

       

- для звена 3      

- для звена 4      

- для звена 5      

3.2. Определение уравновешивающего момента и реакций

в кинематических парах аналитическим методом

3.2.1. Силовой анализ структурной группы 4 – 5

Прикладываем к структурной группе все действующие на нее силы (рис. 5.1). Действие на звено 5 со стороны стойки 0 заменяем реакцией , а на звено 4 со стороны звена 2 – реакцией  в проекциях на оси.

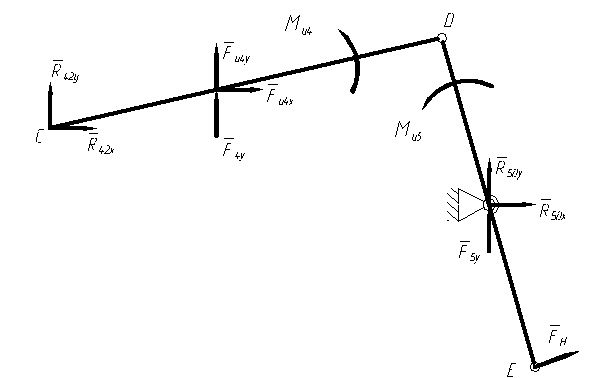
Рис. 5.1. Силовой анализ группы 4 – 5

Для определения реакций в кинематических парах О и С записываем два уравнения проекций сил на координатные оси и два уравнения моментов относительно точки D для звеньев 4 и 5:

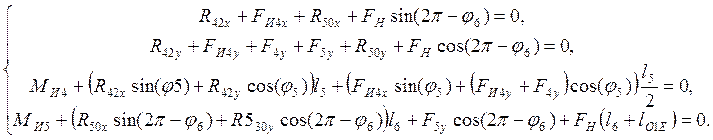(5.1)

Все известные величины переносим в правые части уравнений (5.1). В результате будем иметь:

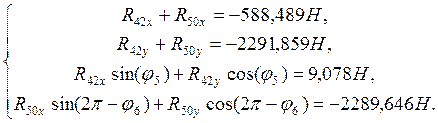                               (5.2)

Решая систему уравнений (5.3) найдем:

,

, .

Реакции  и  определятся соответственно:

Реакцию , действующую в кинематической паре D, находим из уравнения равновесия, например, звена 4:

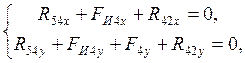
откуда

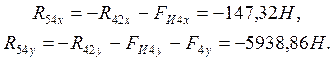
Полная реакция будет:

3.2.2. Силовой анализ структурной группы 2 – 3

Помимо заданных сил на группу действуют реакции ,  и  (рис. 5.2).

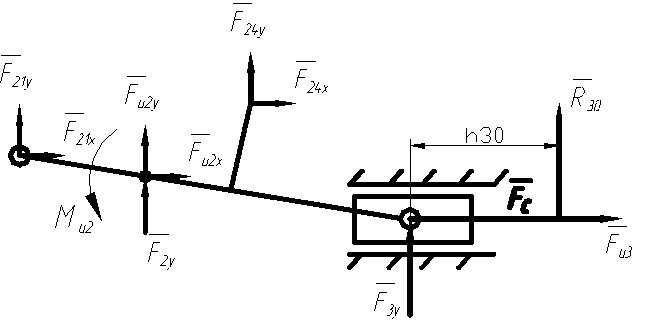
Рис. 5.2. Силовой анализ группы 2 – 3

Силы представлены через их проекции на оси координат. Проекции  и  найдены из анализа предыдущей группы:

, .

Для определения реакции  составим сумму моментов относительно точки A:

;

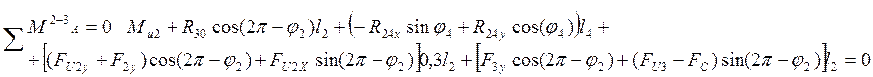
Реакцию , действующую в кинематической паре A, находим из уравнения равновесия звеньев 2-3:

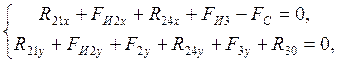
откуда

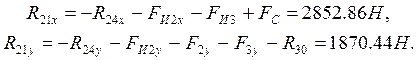
3.2.3 Определение уравновешивающего момента и реакции в кинематической паре О

Составляем уравнения равновесия начального звена механизма (рис. 5.3):

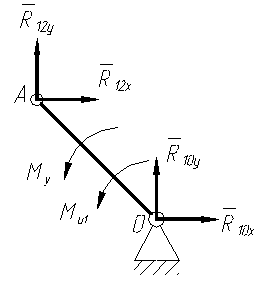
Рис. 5.3. Силовой анализ начального звена

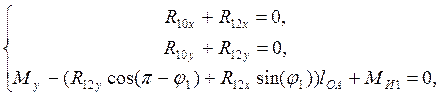                                   (5.2)

где , , ,  – проекции на оси координат реакции на звено 1 стойки 0;  – уравновешивающий момент.

Решая (5.2), найдем:

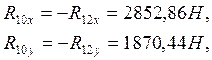
3.3. Определение уравновешивающего момента и реакций

в кинематических парах графическим методом