Анализ и синтез механизмов сенного пресса, страница 2

2.  Радиусом 74 мм проводим тонкой линией траекторию движения начального звена (кривошипа).

3.  Определяем масштабный коэффициент длин

[м/мм],

где l_ОА – истинная длина кривошипа, ОА – выбранный чертежный размер кривошипа, ОА = 80 мм.

=0,005 м/мм.

4.  В соответствии с формулой , находим чертежные и координатные размеры всех остальных размеров механизма, где ВС – чертежная длина звена, например, ВС; l_bc – истинный размер звена.

–   отмечаем на чертеже неподвижные точки О и О₁, рисуем в них вращательные  кинематические пары;

–   проводим окружность радиусом ОА, которая является траекторией движения точки А;

–   строим положения кривошипа, соединяя точку А_i с точкой O;

–   методом засечек строим план положений механизма для каждого положения кривошипа;

Чертежные размеры звеньев.

lOA, мм	lAB, мм	lAC, мм	lCB, мм	lCD, мм	lO1D, мм	lO1E, мм	X, мм	Y, мм
80	272	160	120	112	58	138	152	154

2.4. Кинематическое исследование машин и механизмов аналитическим методом.

Для определения кинематических характеристик механизма применим метод замкнутых векторных контуров.

1.  Рисуем в любом промежуточном положении структурную схему исследуемого механизма.

2.  Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.

3.  В соответствии с методом все звенья механизма, включая стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало оси Х до направления соответствующего вектора.

4.  Полученные векторы объединяем между собой так, чтобы они образовали замкнутые контуры: OABO и OACDO₁O. Причем в каждый контур должно входить не более двух неизвестных величин.

Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора l₁, причем, все векторы совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие  - со знаком «–»:

                                        (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат:

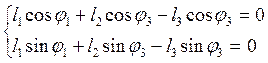                                     (2.2)

Среди величин, входящих в уравнение (2.2), переменными являются углы  j₁  и  j_2. Учитывая, что j₃ =0, преобразуем систему уравнений к следующему виду:

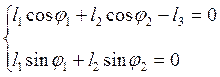.                                       (2.3)

Следовательно, из уравнений (2.3) находим угол наклона вектора `l₂:

                     (2.4)

и модуль вектора `l₃:

                                    (2.5)

Уравнение замкнутости второго контура ОAСDО₁O имеет вид:

                                                                                         (2.6)

или в проекции на оси координат:

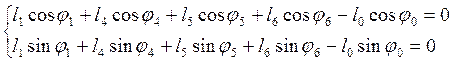.                                         (2.7)

Угол φ₄ определяется как φ₂+a.

Угол a выразим из треугольника ABC:

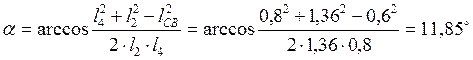                                (2.8)

Следовательно,               φ₄=φ₂+a=3,4º,                                                 (2.9)

Чтобы найти φ₅ рассмотрим дополнительный контур из векторов :

                                        (2.10)

Запишем проекции на оси координат:  

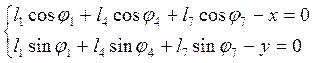.                           (2.11)

Из системы уравнений (2.11) можно определить угол наклона вектора l₇:

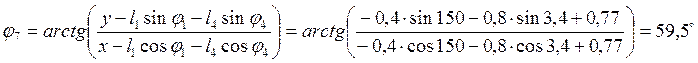 (2.12)

и его модуль

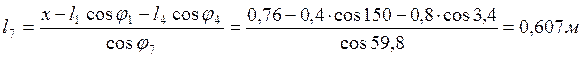                     (2.13)

Зная значения выражений (2.12) и (2.13) можно определить угол φ₅ как φ₇+β. Угол β выразим из треугольника O₁DC:

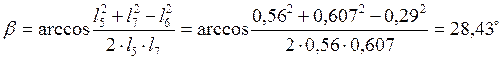                              (2.14)

Следовательно,φ₅=φ₇+β=87,93º.                                                        (2.15)

Исходя из выражений (2.7), (2.9) и (2.15) определим угол φ₆:

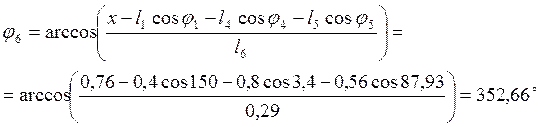            (2.16)

Для определения положений центров масс S₂ и S₄ записываем уравнения замкнутости контуров OAS₂ и OACS₄ .

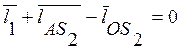                                                                                (2.17)

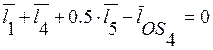                                                                          (2.18)

Из уравнений (2.17) и (2.18) находим координаты центров масс звеньев 2 и 4:

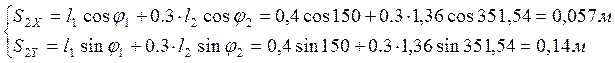,             (2.19)

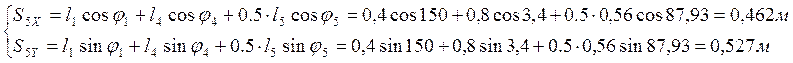
 Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в табл. 2.2.

                      Результаты расчета положений звеньев. Таблица 2.2

. Величина	j1°	j2°	l3, м	j4°	j5°	j6°
Графически	150	351,54	0,999	3,4	87,93	352,66
Аналитически	150	351,54	0,999	3,4	87,93	352,66
Отклонение, D %,	0	0	0	0	0	0

Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.2) и (2.7). После дифференцирования уравнений (2.2) получим:

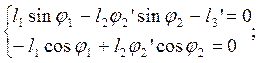                                                                        (2.21)

где j₁’ – аналог угловой скорости звена 1. В расчетах принимаем , так как угловая скорость звена 1 направлена по ходу часовой стрелки; j₂’ – аналог угловой скорости звена 2, l₃’ – аналог поступательной скорости точки В.