Моделирование переходного режима энергосистемы (Лабораторная работа № 9), страница 5

2 10 0. 0.1 0.00002

-2.3936 -82,561

5. 100. 15. 500. 0.1 0.0001 5. 120. 75. 314.1

Результаты расчета переходного режима выводятся программой DIFRK409 в виде таблиц в файлы 09--.REZ и 09--.GRA.

Осциллограммы параметров переходного режима приведены на рис. 4.

2.5. Контроль правильность числового решения дифференциальных уравнений. После окончания переходного режима в электрической схеме устанавливается установленный послеаварийный режим, что можно использовать для контроля правильности числового решения дифференциальных уравнений. Для этого необходимо рассчитать каким-нибудь методом, установленный послеаварийный режим и сравнить получившиеся комплекс. значения параметров с мгновенными значениями соответствующих параметров, которые получаются в результате решения дифференциальных уравнений. Для расчета установленного послеаварийного режима  и снова используем контурные уравнения (контур 1: ветки 1, 3, 5, 6; контур 2: ветки 2, 5, 3 ):

Z₁₁I_к1+Z₁₂I_к2=E_к1

Z₂₁I_к1+Z₂₂I_к2=E_к2                                                                                                                  (19)

где:

Z₁₁=R₁+jwL₃

---

-j(1/(wC₅))+R₆=5+j314,2´0,1-j(1/(314,2´0,0001))+5=

=10+j31,42-j31,84=10-j0,42 Ом;

Z₁₂=Z₂₁=-(jwL₃

---

-j(1/(wC₅)))=-j31,42+j31,84=j0,42 Ом;

Z₂₂=R₂+j(wL₃-1/(wC₅))=500+j(314,2·0,1-1/(314,26´100´10^-6))=

=500-j0,42 Ом;

E_к1=е₁-e₆=E_m1(cosj_e1+jsinj_e1)/Ö2-E_m6(cosj_e6+jsinj_e6)/Ö2=

=100(cos15°+jsin15°)/Ö2-120(cos75°+jsin75°)/Ö2=46,35-j63,66 ‚B.

E_к2=0;

Таким образом, система уравнений (19) в матричной форме с числовыми значениями коэф. и правых частей будет иметь вид:

 

            (10. , -0.42)     (0. , 0.42)             I_к1     (435.35 , -63.66)

(0. , 0.42)        (500.,-0.42      ´   Iк₂    =          (0. , 0.)

Решая эту систему методам Гаусса, получаем неизвестные контурные токи Iк1, Iк2 для  установленного послеаварийного режима:

Iк1=4,893-j6,16 А;

I_к2=-0,00517-j0,00411 А.

Токи в ветках схемы:

I₁=-I₆=I_к1=4,893-j6,167=7,867exp(-j51,54°) А;

I₂=I_к2=-0,00517-j0,00411=0,0066exp(-j141,5°) А;

I

---

₃=I₅=I_к1-I_к2=4,898-j6,156=7,867exp(-j51,49°) А.

Напряжения на  ветках схемы: U₁=I₁Z₁=24,467-j30,8=39,337exp(-j51,5°);

U₂=I₂Z₂=-2,585-j2,057=3,304exp(-j141,5°);

U₃=I₃Z₃=193,36+j153,8=247,11exp(j38,5°);

U₅=I₅Z₅=195,9-j155,9=250,4exp(-j141,5°);

U₆=I₆Z₆=-24,47+j30,8=39,34exp(j128,4°).

e₁=68,31+j18,3=70,72exp(j15°);

e₆=21,96+j81,96=84,86exp(j75°).

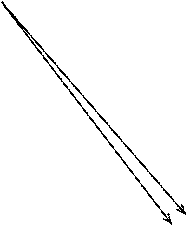
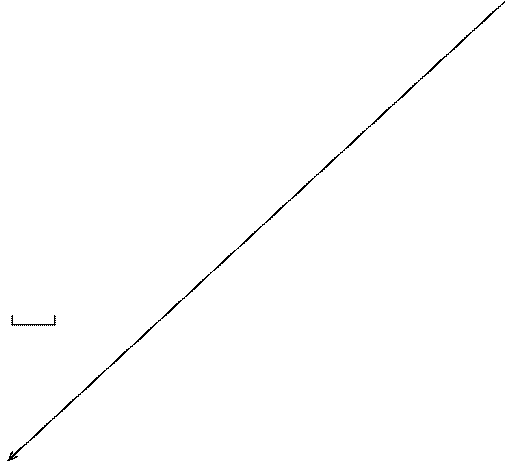
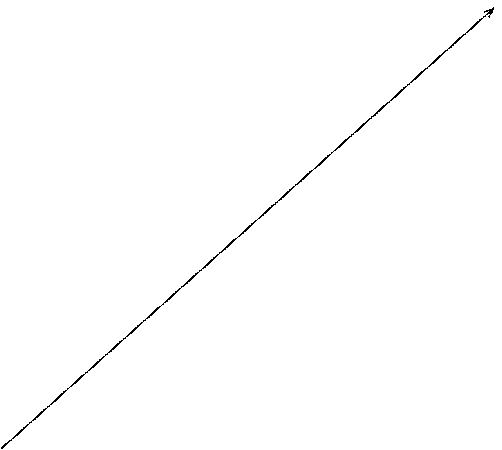
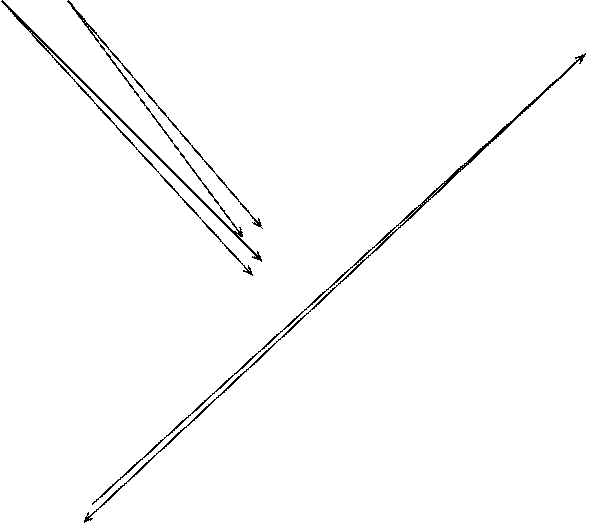
Векторные диаграммы токов и напряжений установленного послеаварийного режима приведены на рис.3. Сравнивая амплитудные ззначения параметров режима на векторной диаграмме ( рис.3) и установленные значения этих параметров на осциллограмме переходного процесса, отмечаем их совпадение и делаем вывод о правильности выполнения числового решения дифференциальных уравнений. Например, читаем с файла 09--.REZ амплитудное значение напряжения u3(t) для t=0,0928 c:

 

U₃

1 A                              I₁=-I

 

                                    I₃=I₅

                        a)                                      I₂

E₁                                                                                              20 B

 

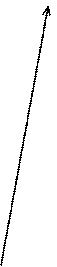E₆

 

                        U₁             U₅

                        U₂

 

U₆

Рис.3.  Векторные диаграммы токов (а) и напряжений (б)

установленного послеаварийного режима в схеме на рис.1.

U3m=351,47 B. Тогда действующее значение U3=351,47/ 2=248,54 B. Соответствующее действующее  значениеU3, получившееся в результате расчета  установленного послеаварийного режима, равно 247,11 В. Разность составляет 0,6 %, что можно пояснить хiбнасцямi при числовых решениях алгебраических и дифференциальных уравнений.

 

3.         Содержание И порядок выполнения работы

При домашней подготовке:

3.1. построить математическую модель для исследования переходного режима методом переменных состояний при замыкании ключа для заданного  варианта схемы на рис.5, взятого с таблицы 1 (номер варианта соответствует номеру бригады). Модернизовать текст программы DIFRK409 (дополнение 1) для ввода входных данных и числового решения вашей системы дифференциальных уравнений. Подготовить файл входных данных для моделирования переходного режима, зарезервировавши в нем место для начальных условий;