Методы решения обычных дифференциальных уравнений (Лабораторная работа № 7)

Министерство образования Республики Беларусь

Белорусская государственная политехническая академия

Кафедра «Электрические станции»

Математические задачи энергетики

Лабораторная работа №7

Методы решения обычных дифференциальных уравнений

Автор Бобко Н.Н.

Минск, 1999

1          Цель работы

Изучение методов, алгоритмов и программ решения обычных дифференциальных уравнений.

2          Теоретические сведения

2.1       Аналитическое  решение дифференциальных  уравнений

Дифференциальным называется уравнение, которое связывает независимую переменную х, неизвестную (искомую) функцию y(x) и ее производные  ,  , … ,   разных порядков:

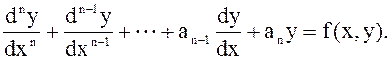                          (1)

Решить дифференциальное уравнение – значит  найти его общий интеграл, который связывает независимую переменную х и неизвестную функцию y(x) с произвольными постоянными величинами  ,  ,...…, , количество которых соответствует порядку n дифференциального уравнения. Общий интеграл в геометрическом смысле  отображается семейством кривых. Для выделения одной из кривых этого семейства (для получения частичного решения) необходима определить произвольные постоянные величины  ,  ,…..., , задаваясь начальными условиями.

Когда коэффициенты  ,  ,...,   не зависят от искомой функции у(х), то уравнение (1) является линейным. Уравнение (1) является уравнением с постоянными коэффициентами, когда коэффициенты  ,  ,...,   - числовые константы. При f(y,x)=0 уравнение называется однородным. Уравнение (1) удерживает одну независимую переменную х, потому оно называется обычным дифференциальным уравнением. Когда дифференциальное уравнение удерживает более, чем одну независимую переменную и, соответственно, более чем одну искомую переменную и ее производные, то такое уравнение называется дифференциальным уравнением в частных производных.

Для интегрирования уравнения с постоянными коэффициентами надо найти корни соответствующего ему характеристического уравнения

                              (2)

Когда все корни  ,  ,...,  характеристического уравнения разные, то общее решение однородного уравнения, соответствующего уравнению (1), есть сумма частичных решений

     (3)

Начальными условиями уравнения (1) называются числовые значения неизвестной функции у(х) и ее производных  ,  ,...,  при значении независимой переменной х, равной нолю:

;  ; ..., 

Задача с начальными условиями называется задачей Коши (в отличия от задачи с предельными условиями, когда задаются значения неизвестной функции в двух предельных узлах независимой переменной). Для того, чтобы из общего решения получить частичное решение, необходимо решить систему линейных алгебраических уравнений относительно постоянных ,  ,..., : 

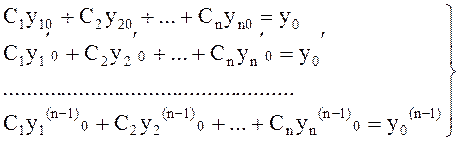
Когда частичные решения , ,...,  линейно независимые, то детерминант этой системы (детерминант Вронского) не равный нолю и решение системы существует.

Общее решение линейно независимого уравнения n-ого порядка с первой частью складывается из общего решения соответствующего ему однородного уравнения и какого-либо частичного решения уравнения (1).

Пример 1. Найти аналитическое решение дифференциального уравнения (4), которое описывает переходный процесс при включении индуктивной катушки на переменное напряжение (рис. 1) при i(0)=0:

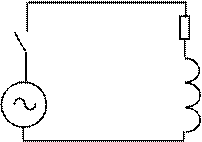S                         R 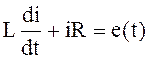                    (4)

е(t)          L

Рис.1.

Индуктивность катушки L (Гн) и ее активное сопротивление R (Ом) не являются здесь функциями неизвестного тока i(t) , потому уравнение (4) является обычным линейным неоднородным дифференциальным уравнением первого порядка. Потому решение этого уравнения может быть найдено в аналитической форме. Электродвигающая сила e(t) источника электрической энергии является заданной функцией независимой переменной - времени t:

е(t)=Emsin( t+ e), где  - амплитуда синусоидального сигнало e(t), В;

w- угловая частота сигнала e(t), рад/с;

j_е - фазовый сдвиг сигнала e(t) в момент замыкания ключа S, град.

Переходной ток в цепи, как известно, складывается со свободной  и  принудительной   составляющих:

i= + .                                                                                           (5)

Свободная составляющая і_св - это решение однородного (при e(t)=0) уравнения (4). Принудительная составляющая і_пр - это частичное решение неоднородного  уравнения (4).

Найдем свободную составляющую. Для этого составим характеристическое уравнение для (4):

La+R=0.

Его единственный корень

 .

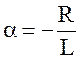Тогда свободная составляющаяя тока в схеме при замыкании ключа S:

.

Принудительную составляющую найдем как установленный ток, который протекает в схеме после окончания переходного режима, когда переходная составляющая загаснет:

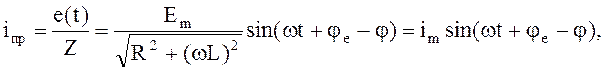
где        - амплитуда принудительной составляющей тока в схеме;

j - угол фазового сдвига векторов e(t) и  (t).

Тогда полный ток переходного режима в соответствия из (5):

                                 (6)

Постоянную интегрирования С определим, использовав начальное условие i(t=0)=0. Подставим ее в выражение (6) и получим:

Тогда ток переходного режима примет окончательный вид:

где  t=L/R - постоянная времени RL-контура схемы, с.