Методы решения обычных дифференциальных уравнений (Лабораторная работа № 7), страница 2

Таким образом, в переходном режиме схемы на установленный синусоидальный  ток   накладывается экспоненциальный  свободный ток  .

2.2 Числовые методы решения  дифференциальных уравнений.

В примере 1 использован классический метод решения дифференциальных уравнений. Решение в виде аналитической функции является точным. Его удобно исследовать аналитическими методами, дифференцировать, интегрировать, находить экстремумы и т.д. Однако этот метод непригоден  для нелинейных уравнений, которые чаще всего являются основой для построения математических моделей переходного режима электроэнергетической системы. Для интегрирования таких уравнений разработаны  численные методы.

Численные методы обладают вычислительной и методической погрешностью, при их реализации возникает проблема устойчивости и сходимости вычислительного процесса. Стандартные процедуры численного решения разработаны  для нормальной (канонической) формы представления дифференциального уравнения: уравнение имеет  первый  порядок и решено относительно производной:

                                              (7)

Дифференциальное уравнение n-ого порядка можно свести к системе n уравнений первого порядка, а стандартные подпрограммы решения дифференциальных уравнений первого порядка распространяются на системы таких уравнений.

При численном решении дифференциального уравнения на интервале [x₀, x_n] сходимости независимой переменной х выбирается некоторое множество узлов, которое называется сеткой:

в которых высчитываются приближенные значения  ,  ,...,  ,...,   искомой функции у(х). Иначе говоря, решение строится в виде числовой таблицы . Разность   называется шагом сети. Часто шаг сети выбирают постоянным.

Когда для вычисления решений    используется несколько предварительно вычисленных значений    ...…,  , то числовой метод называется многошаговым  (r-шаговым). Когда r=0, то метод называется одношаговым.

Одношаговые методы (методы Рунге-Кутта) легко программируются. Можно легко изменить величину шага h во время вычисления, они являются самостартующими. Недостатками одношаговых  методов являются значительные затраты машинного времени на многоразовое вычисление правой части f(у,x) на каждом шаге, а также отсутствие точной формулы для определения ошибки при вычислении неизвестной функции  .

Многошаговые  методы (Адамса, Милна) позволяют значительно уменьшить количество вычислений на каждом шаге за счет использования значений функции    … , получившихся на предыдущих шагах. Однако для организации начала вычислений необходимо применять специальный стартовый алгоритм, в качества которого используются одношаговые методы. К многошаговым числовым методам принадлежат также методы прогноза и коррекции (метод Хемминга). Многошаговые  методы требуют применения стартового алгоритма не только на начале вычисления, но и при скачкообразных изменениях интегрируемой  переменной (короткие замыкания, коммутации и т.д.), потому для решения дифференциальных уравнений, которые описывают переходный процесс в энергосистеме, применяются преимущественно одношаговые  методы, которые и рассматриваются в этой работе.

Для построения числовых формул, которые аппроксимируют дифференциальное уравнение, y’ =f(y,x) используется разложение  решения в ряд Тейлора в окрестности узла  :

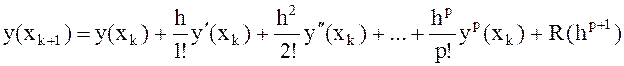 .     (7)

Числовой метод имеет порядок  p,  когда его расчетная формула удерживает составы ряда  Тейлора с шагом h в степени p.

2.3       Метод Эйлера

Метод Рунге-Кутта первого порядка называется методом Эйлера. Формула Эйлера получается, когда в ряде Тейлора отбросить все составы в правой части, кроме первых двух:

                                      (8)

Тут вместо производной    подставлена правая часть уравнения (4). Формула (8) соответствует числовому интегрированию функции f(x,y) по способу  правых прямоугольников (для расчета    используется значение функции    для к-ого узла). Потому формулу (8) называют явным методам Эйлера (правая часть (8) не удерживает неизвестных величин). Неявный метод Эйлера заключается в вычислении интеграла функции f(y,x) по способу левых прямоугольников  (в формулу (8) подставляются значения функции для (к+1)-го узла):