Методы решения обычных дифференциальных уравнений (Лабораторная работа № 7), страница 3

                                 (9)

Для использования формулы вида (9) необходима на каждом временном шаге или решить алгебраическую систему, составленную из уравнений (9) для всех узлов   (метод прогонки), или применить итерационные методы, потому что неизвестная величина   входит  одновременно в правую и левую части уравнения (9).

2.4       Методы Рунге-Кутта

Для повышения точности необходимо удерживать большее, чем в методе Эйлера, количество составов ряда  Тейлора, однако при этом возрастает порядок производных, какие необходимо вычислить. Рунге предложил вместо вычисления производных использовать вычислительный алгоритм в следующем виде:

 , где функция  j (x,y,h) аппроксимирует отрезок ряда Тейлора с точностью сдачи  . Метод Рунге-Кутаы второго порядка для уравнения  имеет  вид:

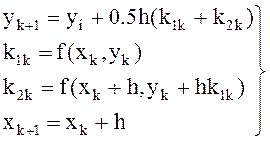 .                                                              (10)

Этот алгоритм удерживает составы ряда Тейлора, в которые входит  h²,  и требует двукратного вычисления правой части f(y,x) уравнения на каждом временном шаге.

Наиболее часто применяется метод Рунге-Кутта четвертого порядка:

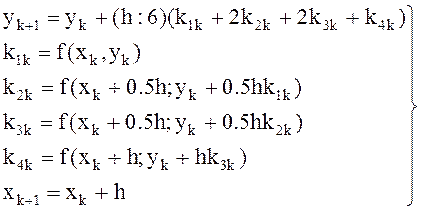 .                                     (11)

Этот метод требует четырехкратного вычисления правой части дифференциального уравнения на каждом шаге.

Алгоритмы (8), (9), (10), (11) легко распространяются на системы дифференциальных уравнений, предоставленных в нормальной форме. При этом на каждом временном шаге исполняется параллельное вычисление всех интегрируемых переменных, которые входят в систему. Например, метод Рунге-Кутта  второго порядка для системы двух уравнений

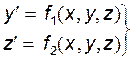                                                                                       (12)

будет заключаться в выполнения следующих действий на каждом (к+1)-ом временном шаге:

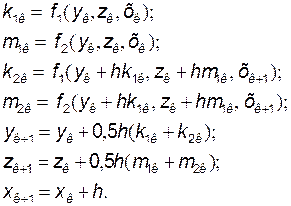                                                                        (13)

3.         Программы DIFEIL, DIFRK2, DIFRK4

В приложениях 1, 2, 3 приведенный тексты программ DIFEIL, DIFRK2, DIFRK4 на алгоритмическом языке ФОРТРАН, которые позволяют соблюсти численное решение системы дифференциальных уравнений

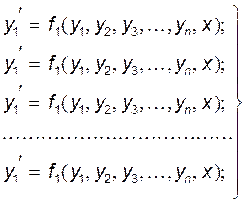
соответственно методами Эйлера, Рунге-Кутта второго и Рунге-Кутта четвертого порядка с постоянным шагом h. Каждая из этих программ  имеет главный модуль, подпрограмму реализации метода и подпрограмму вычисления правых частей  ,  ,...…, .

Главные модули программ идентичные. Они обеспечивают  организацию чтение входных данных из файлов на диске, возрастание независимой переменной, контроль окончания расчета и запись результатов в выходной файл на диск.

Подпрограммы EILER, RNGKT2, RNGKT4 исполняют все операции для реализации вычислений на одном временном шаге.

Подпрограммы PRAV для каждой системы дифференциальных уравнений являются оригинальными и создаются пользователем программ в соответствии с видом правой части системы уравнений, которая решается.

4.         Порядок выполнения работы

4.1.      При домашней подготовке необходимо получить аналитическое решение дифференциального уравнения первого порядка (решить дифференциальное уравнение классическим методам), которое описывает переходный процесс после коммутации ключа S в RL- или RC-схеме, в соответствия с вариантом, приведенным в табл. 1.

4.2.      Изучить структуру и содержание двух заданных в табл. 1 программ, составить их блок-схемы. Написать текст подпрограммы PRAV для решения дифференциального уравнения заданного варианта. Подготовить файл входных данных.

4.3.      Дополнить тексты программ блоком для вычисления значений аналитического уравнения. Дополнить также программы формулой для вычисления относительной погрешности  числового метода:

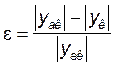 , где       y_ак - точные значимости искомой функции y(t) в к-тых узлах оси t, получившиеся по аналитической формуле;

y_к- приблизительные значения искомой функции y(t) в тех же узлах оси t, получившиеся в итога числового решения уравнения.