Лабораторная работа №4
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Цель работы: 1. Установить зависимость углового ускорения от момента силы при определенном моменте инерции системы.
2. Определить момент инерции системы.
Приборы и принадлежности: маятник Обербека, штангенциркуль, отвертка, секундомер, длинная линейка, набор грузов.
1. ОБЩИЕ СВЕДЕНИЯ
 Вращательное движение, как и поступательное,
описывается вторым законом Ньютона. В применении к вращательному движению он
носит название основного закона динамики вращательного движения.
Вращательное движение, как и поступательное,
описывается вторым законом Ньютона. В применении к вращательному движению он
носит название основного закона динамики вращательного движения.
Этот закон устанавливает зависимость между суммарным моментом сил М, действующих на тело, моментом инерции тела I и приобретаемым угловым ускорением ε.
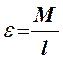 или
или ![]() (1)
(1)
![]() Уравнение (1) - основное уравнение динамики
вращательного движения.
Уравнение (1) - основное уравнение динамики
вращательного движения.
Угловое ускорение зависит прямо пропорционально от момента силы
ε ~ М
и обратно пропорционально от момента инерции
ε ~ 1/ I.
Если сравнить с поступательным движением, то момент силы М аналогичен силе, так как изменяет состояние тела, момент инерции I аналогичен массе тела. Момент инерции является мерой инертности тела при вращательном движении.
2. ФИЗИЧЕСКИЕ ОСНОВЫ ЭКСПЕРИМЕНТА
Чтобы установить зависимость между моментом силы М и угловым ускорением ε, нужно экспериментально определить каждую из этих величин.
Рассмотрим задачу о вращении маятника Обербека.
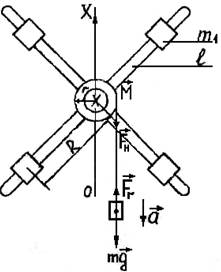
Если груз m, подвешенный на нити, достаточно велик, то он движется равноускоренно вниз. При этом крестовина вращается с угловым ускорением ε (рис. 1).
По второму закону Ньютона для груза составляем уравнение динамики
![]() (2)
(2)
где a - линейное ускорение, м/с2; Fr - сила реакции нити, приложенная к грузу, Н; mg - сила тяжести груза, H.
В то же время к шкиву приложена сила Fн - сила натяжения нити, причем, но третьему закону Ньютона Fн = -Fr, сила натяжения нити равна силе реакции нити. Значение F определим, спроецировав уравнение (2) на ось ОХ
- ma = Fr – mg;
Fr = mg – mа.
Так как Fн = Fr,
Fн = mg - ma. (3)
Для вращающейся крестовины применяем основное уравнение динамики вращения М = Iε.
Момент силы М создается касательной к шкиву силой Fн, направление момента силы определяем по правилу правого винта (на рисунке М направлен за чертеж, что отмечено знаком X).
По определению момента силы ![]()
где r - плечо силы, м.
Подставив вместо Fн ее выражение (3), получим
M = m(g - a)r. (4)
Угловое ускорение ε связано с тангенциальным ускорением соотношением
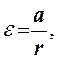 (5)
(5)
Линейное ускорение а определяем из следующих соображений. В начальный момент времени скорость падения груза m равна 0. Если t - время падения груза с высоты h, то
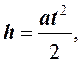
откуда
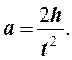 (6)
(6)
Подставив формулу (6) в формулы (4) и (5), получим
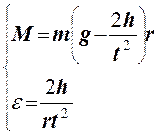 (7)
(7)
Момент инерции крестовины можно рассчитать по формулам, зная длину и массу стержней, а также массу цилиндров m1 и их расстояния до оси вращения (рис. 1)
Iкр = Iц +Iст,
где Iкр - момент инерции крестовины, кг · м2; - суммарный момент инерции цилиндров m1, кг · м2; Iст - суммарный момент инерции стержней, кг · м2.
Iц = 4m1·R2, где m1 - масса одного цилиндра, кг; R - расстояние цилиндра до центра вращения, м.
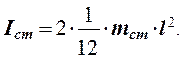
где mст - масса одного стержня, кг; l - длина одного стержня, м. Окончательная формула момента инерции принимает вид
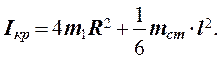 (8)
(8)
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1
Исследовать зависимость углового ускорения от момента силы.
1) Установите с помощью отвертки цилиндры m1 на одинаковых расстояниях от центра вращения и закрепите их в этом положении на крестовине.
2) Измерьте линейкой высоту h падения груза m на нити.
3) Измерьте штангенциркулем диаметр шкива d´ - с намотанной нитью и d´´ - без нити, после чего найдите среднее арифметическое значение радиуса шкива
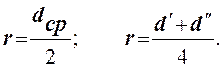
4) Подвешивая поочередно на нить грузы различной массы, измерьте секундомером время t падения каждого груза с высоты h. Время падения каждого грузя следует измерить пять раз и найти среднее арифметическое tср
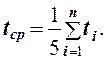
Измерения произведите для 5-6 грузов. Результаты занесите в табл. 1
Таблица 1.
Результаты измерений
|
Номер опыта |
d´, м |
d´´, м |
r, м |
ti, с |
tср, с |
m, кг |
ε, с-2 |
M, Н·м |
|
1 |
||||||||
|
… |
||||||||
|
5 |
5) По формулам (7) произведите расчет ε и М, также занесите их в табл. 1.
6) По данным табл. 1 постройте график зависимости ε(М) на миллиметровой бумаге (рис. 2).
Задание 2
Вычислить момент инерции крестовины.
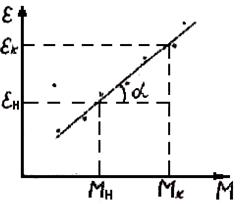 Для экспериментального определения момента инерции крестовины
следует из графика найти
Для экспериментального определения момента инерции крестовины
следует из графика найти
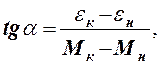
где tgα - тангенс угла наклона графика к оси абсцисс; εк, εн, Mк, Мн - координаты точек графика, отстоящих достаточно далеко друг от друга.
Момент инерции определите по формуле
|
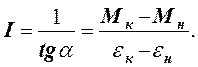
Для теоретического расчета момента инерции используйте формулу (8). Данные измерений и расчета занесите в табл. 2.
Таблица 2
Результаты измерений
|
m1, кг |
R, м |
mст, кг |
l, м |
I, кг · м2 |
Определите ΔI = │Iт - Iкр│, где ΔI' - разность между теоретическим и экспериментальным значениями момента инерции крестовины. Вычислите относительную ошибку.
Проанализируйте возможное несовпадение результатов. Выводы анализа запишите в отчет.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1) Как сформулировать основной закон динамики вращения?
2) Как записать основное уравнение динамики вращения?
3) Как зависят величины, входящие в основное уравнение динамики вращения, друг от друга?
4) Как экспериментально определить момент инерции крестовины?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.