Лабораторная работа 7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: определить момента инерции твердого тела методом крутильных колебаний.
Оборудование: лабораторная установка - крутильный маятник.
1. ОБЩИЕ СВЕДЕНИЯ
 Вращательным движением твердого тела называется такое
движение, при котором все точки тела описывают окружности, центры которых
лежат на одной прямой, называемой осью вращения
Вращательным движением твердого тела называется такое
движение, при котором все точки тела описывают окружности, центры которых
лежат на одной прямой, называемой осью вращения
В твёрдом теле все точки жестко связаны между собой и могут вращаться вокруг неподвижной оси под действием момента внешней силы. При этом вектор момента силы М и вектор углового ускорения ε всегда направлены в одну сторону и справедлив основной закон динамики вращательного движения
![]() M = I ε
M = I ε
где I - момент инерции твердого тела относительно неподвижной оси вращения, кг· м2.
Момент инерции I характеризует инертные свойства твердого тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
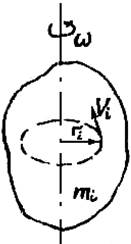
Рассмотрим твёрдое тело и выделим в нём материальную точку массой mi. Её удаление от оси вращения обозначим через ri (рис. 1). Тогда линейная скорость этой точки равна
vi = ωi ri, где ωi - угловая скорость вращения, рад/с.
Момент импульса относительно оси вращения равен
Li = miViri = miriωi.
Величина равная Ii = miri2 называется моментом инерции материальной точки.
Для твёрдого тела моменты импульсов складываются по всем материальным точкам, образующим это тело. Тогда суммарный момент импульса равен
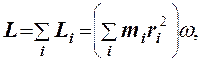
или
L = Iω.
Здесь
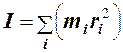
и есть момент инерции твердого тела относительно оси вращения.
Суммирование производится по всем материальным точкам, входящих в твердое тело.
Практически вычисление такой суммы сводится к вычислению соответствующего интеграла, что для однородных тел симметричной формы труда не составляет, то есть
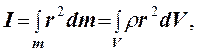
где ρ - плотность, кг/м3, V - объем, занимаемый телом, м3.
 Интегрирование производится по всему объёму тела.
Интегрирование производится по всему объёму тела.
Для любого твёрдого тела можно указать три взаимно перпендикулярные оси, проходящие через его центр инерции. Эти оси называются главными осями тела. А момент инерции относительно любой оси вращения выражается через моменты инерции тела относительно этих главных осей.
![]() Главные
оси просто определить для однородных симметричных тел (шара, куба,
параллелепипеда и т.д.). Главные оси инерции таких тел всегда совпадают с осями
симметрии тела.
Главные
оси просто определить для однородных симметричных тел (шара, куба,
параллелепипеда и т.д.). Главные оси инерции таких тел всегда совпадают с осями
симметрии тела.
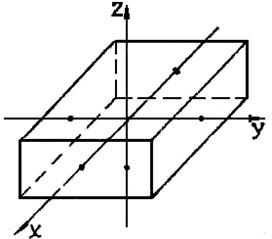
Например, главные оси однородного прямоугольного параллелепипеда проходят через его геометрический центр перпендикулярно граням (рис. 2).
 Для тел сложной формы главные оси и моменты инерции
определяют экспериментально.
Для тел сложной формы главные оси и моменты инерции
определяют экспериментально.
Если известны главные оси твердого тела, то с ними связывают прямоугольную систему координат О, X, У, Z. Начало координат находится в центре инерции твердого тела.
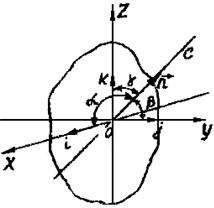
Возьмём произвольную ось вращения, проходящую через центр инерции, ось ОС (рис. 3).
![]() Момент инерции тела относительно оси ОС
выражается через моменты инерции главных осей, то
есть
Момент инерции тела относительно оси ОС
выражается через моменты инерции главных осей, то
есть
I= Ix cos2 α + Iy сos2 + Iz cos2 γ (1)
где Ix, Iy, Iz - моменты инерции тела относительно осей ОХ, OY, OZ; α, β, γ - углы между осью вращения и осями прямоугольной системы координат.
Моменты инерции Ix, Iy, Iz определяются экспериментально. Момент инерции тела относительно произвольной оси вращения находится простым суммированием по формуле (1).
Момент инерции тела зависит от выбора оси вращения. Однако это не значит, что для всякой новой оси момент инерции следует вычислять заново.
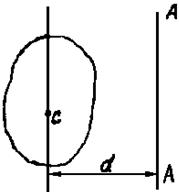
Если известен момент инерции тела относительно оси, проходящей через центр инерции, то момент инерции тела относительно любой оси, параллельной первой и смещенной на расстояние d, находится по теореме Штейнера (рис. 4):
![]()
где I0 - момент инерции относительно оси вращения, проходящей через центр инерции, кг · м3; m - масса тела, кг; d - расстояние между осями, м.
Используемый в лабораторной работе крутильный маятник позволяет определить момент инерции тел любой формы.
 Такой маятник представляет собою рамку, подношенную на
тонкой упругой струне. При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
Такой маятник представляет собою рамку, подношенную на
тонкой упругой струне. При повороте рамки из положения равновесия на некоторый
угол Θ, со стороны нити на нее действует упругий момент равный
Mупр = -D Θ, где Θ - угол поворота рамки, рад; D - коэффициент, характеризующий момент упругих сил, Н · м.
![]() При достаточно тонкой и длинной струне зависимость М(Θ)
выполняется и для больших углов поворота, а затухания при крутильных колебаниях
можно считать малыми.
При достаточно тонкой и длинной струне зависимость М(Θ)
выполняется и для больших углов поворота, а затухания при крутильных колебаниях
можно считать малыми.
Пренебрегай затуханиями, движение рамки записывают уравнением для свободных незатухающих колебаний
![]()
или
![]() (2)
(2)
где
![]() - угловое
ускорение, рад · с2, вторая производная по времени от угла попорота;
ω0 - циклическая частота колебаний, рад/с. Циклическая частота
колебаний выражается как
- угловое
ускорение, рад · с2, вторая производная по времени от угла попорота;
ω0 - циклическая частота колебаний, рад/с. Циклическая частота
колебаний выражается как
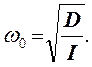
Период таких колебаний равен
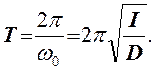 (3)
(3)
Решение дифференциального уравнения (2) имеет вид
![]()
где Θ0 - угловая амплитуда колебаний, рад; α - начальная фаза колебаний, рад.
Если известен момент инерции I, то найти период колебаний рамки не составляет труда, а следовательно, и найти постоянную D. И наоборот, зная постоянную D, используя формулу (3) можно рассчитать момент инерции тела.
В данной лабораторной работе постоянная D не определяется. Для нахождения момента инерции рамки используется тело с известным моментом инерции. В качестве такого тела взят куб с достаточно идеальными поверхностями и гранями. Его момент инерции относительно оси, походящей через центр, вычисляется по формуле
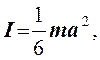 (4)
(4)
где m - масса куба, кг, а - сторона куба, м.
Такой куб жестко закрепляется в рамке крутильного маятника. Если вывести нагруженную рамку из положения равновесия, то она будет совершать крутильные колебания, а её период колебаний равен
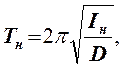
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.