Определение адиабатной постоянной

Лабораторная работа №10

ОПРЕДЕЛЕНИЕ АДИАБАТНОЙ ПОСТОЯННОЙ

Цель работы: определить адиабатную постоянную для воздуха.

Приборы и принадлежности: баллон, кран, манометр, клапан, соединительные трубки и шланги.

1. ОБЩИЕ СВЕДЕНИЯ

Теплоемкостью тела С называется физическая величина, численно равная количеству теплоты, необходимому для нагревания  тела на один Кельвин:

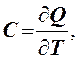
где С - теплоемкость тела, Дж/К;  - количество теплоты, Дж;  - изменение температуры, К.

Для практического использования удобны теплоемкость единицы массы (удельная) и теплоемкость моля (молярная).

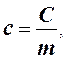
где с - удельная теплоемкость вещества, Дж/(кг·К); m - масса тела, кг.

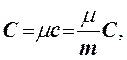
где С - молярная теплоемкость, Дж/(моль·К); μ - масса моля вещества, кг/моль.

Теплоемкость зависит от вида процесса, происходящего в веществе. Особенно ярко эта зависимость проявляется в газах. Так, например, при изохорическом (объем V = const) процессе газ не совершает работы (δА = PdV = 0,  P - давление) и, следовательно, всё тепло идет на увеличение внутренней энергии U в соответствии с первым началом термодинамики:

δQ_V = dU, где δА - элементарная работа, Дж; δQ - элементарное количество теплоты, Дж; dU - дифференциал внутренней энергии, Дж. Изохорическую теплоемкость обозначим C_V.

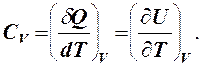
Внутренняя энергия идеального газа не зависит от объема, следовательно,

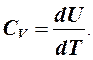                                                        (1)

При изобарическом (P = const) нагревании газ расширяется и совершает работу над окружающими телами. При этом часть полученной теплоты расходуется на совершение работы и для нагревания газа на 1К необходимо большее количество теплоты.

δQ_P = dU + PdV.

Изобарическую теплоемкость обозначим С_P.

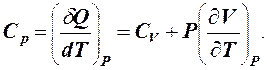                                             (2)

Для моля газа при P = const из уравнения Клапейрона - Менделеева PV = RT находим

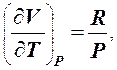                                                    (3)

где R = 8,31 Дж/(моль·К) - универсальная газовая постоянная, численно равная работе, совершаемой молем идеального газа, при его изобарическом нагревании на один Кельвин. Запишем формулу (1) для моля газа и подставим в него (2)

                                                                 C_P = C_V + R.                                                  (4)

Полученное равенство называетcя уравнением Майера.

Молярные теплоемкости можно рассчитать, используя результат теоремы о равномерном распределении энергии по степеням свободы молекул. Степенями свободы называются независимые координаты, необходимые для задания движения частицы. Число степеней свободы обозначим i. На одну степень свободы приходится средняя кинетическая энергия равная kТ/2. Здесь k = R/N = 1,38·10^-23 Дж/К - постоянная Больцмана, N = 6,02· 10²³ моль^-1 - число Авогадро, то есть число молекул в моле вещества. Средняя энергия молекулы газа равна ikТ/2, внутренняя энергии моля

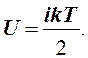
Отсюда с помощью (1) и (4) получаем

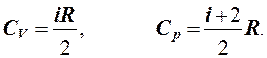
Отношение теплоемкостей называется адиабатной постоянной

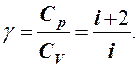                                              (5)

Адиабатная постоянная играет важную роль в термодинамике. С ее помощью записываются уравнения адиабатных процессов, вычисляется скорость звука в газах, определяется теплоемкость политропических процессов и т.д.

2. ОПИСАНИЕ УСТАНОВКИ

Для определения γ в рассматриваемой работе используется адиабатическое расширение газа. Адиабатным называется процесс, происходящий без теплообмена с окружающей средой Хорошим приближением к адиабатному является быстро протекающий процесс.

Схема установки для определения адиабатной постоянной изображена на рис. 1.

Насосом II воздух накачивается в баллон Б до небольшого избыточного давления, регистрируемого манометром М. Клапан Кл препятствует выходу газа через систему накачки. Кран Кр позволяет быстро выпустить избыток воздуха из баллона.

Обозначим температуру окружающего воздуха через Т₁, атмосферное давление – P₀. Давление в баллоне, после того как в него накачали воздух,   обозначим Р₁: