Определение момента инерции твердого тела методом крутильных колебаний, страница 2

где Т_н - период колебаний нагруженной рамки, с; I_н - момент инерции системы состоящей из рамки и куба, кг· м².

Момент инерции рамки с кубом очевидно, равен

I_н = I_р +I_к.                                                  (5)

где I_р - момент инерции рамки, кг· м²; I_к - момент инерции куба, кг· м². С учетом (5) период колебаний нагруженной рамки запишется как

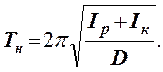                                          (6)

Если колебания совершаются свободной рамкой без куба, то её период колебаний равен

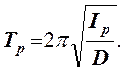                                               (7)

Уравнения (6) и (7) позволяют исключить неизвестную постоянную D.

В результате имеем

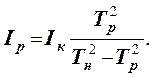
Зная момент инерции свободной рамки, можно найти момент инерции любого тела. Для этого достаточно определить периоды колебаний рамки и рамки с телом, а затем рассчитать момент инерции исследуемого тела.

Рассмотрим рамку с исследуемым телом как систему. Суммарный момент инерции такой системы равен

I_с = I_р + I_т, где I_т - момент инерции исследуемого тела, кг · м².

Зная период колебаний рамки с телом, находим момент инерции системы но формуле

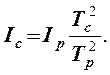                                                    (8)

где Т_с - период колебаний системы (рамка с исследуемым телом), с.

Момент инерции исследуемого тела вычисляется как разность

I_т = I_с - I_р.                                                     (9)

или                                                         I_т 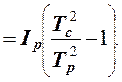                                               (10)

Формула (10) получена после замены в (9) суммарного момента, инерции системы его значением I_с из формулы (8).

2. ОПИСАНИЕ КРУТИЛЬНОГО МАЯТНИКА

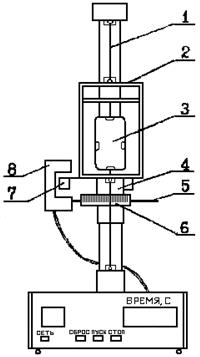
В лабораторной работе момент инерции тел определяется с помощью крутильного маятника путём вычисления периода колебаний его рамки (рис. 5).

Твёрдое тело закрепляется в рамке 2, подвешенной на стальной струне 1. При отклонении рамки от положения равновесия она совершает крутильные колебания. Плита 5 служит основанием для фотоэлектрического датчика 8,   электромагнита 4 и угловой шкалы 6. Электромагнит фиксирует рамку в начальном положении. После нажатия кнопки «Пуск» освобождается рамка с грузом 3. При движении рамки стрелка 7 пересекает свет фотоэлектрического датчика 9. Возникающие импульсы датчика передаются миллисекундомеру и высвечиваются на цифровом индикаторе. После нажатия кнопки «Стоп» и завершения полного периода последнего колебания рамки миллисекундомер прекращает подсчёт импульсов. На его цифровом индикаторе фиксируются число полных колебаний рамки n и продолжительность колебаний t. Период колебаний рамки определяется как 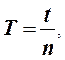где t - время колебаний рамки, n - полное число колебаний.            

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1) Определение момента инерции рамки крутильного маятника.

а) С помощью миллисекундомера найдите число и время полных колебаний рамки без груза, порядка 10 колебаний.

б) Рассчитайте период колебаний ненагруженной рамки как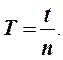

в) Определите период колебаний рамки с эталонным телом - кубом, Т_н. Для этого предварительно закрепите куб в рамке относительно оси, проходящей через центр инерции.