



Тема 6. Числовые характеристики функций случайных величин.
В практических задачах часто встречаются вопросы, требующие
оценки числовых характеристик функций СВ. Простейший случай нам
встречался, например, вычисление значения начального момента порядка 2 (α2).
Известно, что 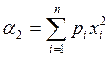 , где
, где ![]() ,
а X – дискретная СВ, заданная своим рядом
распределения. Напомним, что в этом случае значения
,
а X – дискретная СВ, заданная своим рядом
распределения. Напомним, что в этом случае значения ![]() имели
ряд значений вероятностей pi, эквивалентных
для соответствующих xi,
имели
ряд значений вероятностей pi, эквивалентных
для соответствующих xi, ![]() , т.е. вероятности самих СВ и функций
совпадали.
, т.е. вероятности самих СВ и функций
совпадали.
Другого типа задача: на вход технического устройства поступает случайное воздействие X, которое преобразуется по некоторому закону φ и на выходе мы имеем СВ вида Y=φ(X). При известном законе распределения СВ X необходимо найти числовые характеристики СВ Y. См. Схемы:

В описанных случаях могут возникнуть три типа задач:
1. Зная закон распределения СВ X, найти закон распределения СВ Y, естественно это можно обобщить на системы СВ.
2. Зная закон распределения СВ X, найти числовые характеристики СВ Y (или системы).
3. Зная числовые характеристики СВ X, найти числовые характеристики СВ Y.
Рассмотрим методы решения задач типа 2 и 3.
Пусть СВ Y зависит функционально от СВ X, т.е.
Y=φ(X).
Схема решения такой задачи такова:
Для дискретного случая :
Дано:
|
X: |
x1 |
x2 |
… |
xi |
… |
xn |
|
p1 |
p2 |
… |
pi |
… |
pn |
Это ряд распределения для СВ X
где ![]() ,
, ![]()
![]() и
и ![]()
При X=xi имеем Y=φ(xi) и вероятность этого события равна pi. Можно записать таблицу вида:
|
φ(x1) |
φ(x2) |
… |
φ(xi) |
… |
φ(xn) |
(6.1) |
|
p1 |
p2 |
… |
pi |
… |
pn |
Но это еще не ряд распределения для СВ Y.
Необходимо построить ΣY={y1, y2,…} и
объединить одинаковые значения ![]() на совокупности функций
φ(xi), присваивая им вероятность как
сумму составляющих.
на совокупности функций
φ(xi), присваивая им вероятность как
сумму составляющих.
Но если речь идёт о расчёте M[Y] и D[Y], то можно воспользоваться таблицей в виде (6.1). Действительно, имеем
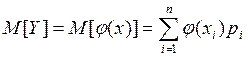 ,
,
![]() , где
, где ![]()
или в координатной форме
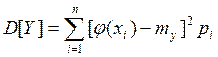
Аналогично определяются начальные и центральные моменты s-го порядка:
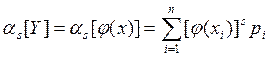 и
и 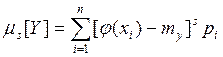
Для непрерывного случая при известной плотности f(x) имеем:
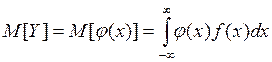 ;
;
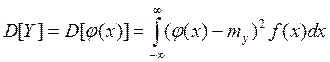 ;
;
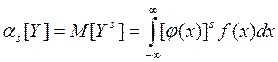 ;
;
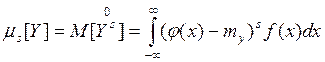
Таким образом, по закону распределения аргумента X есть возможность найти числовые характеристики функции вида Y=φ(X).
Расчётные формулы, аналогичные приведённым, можно привести и для функции нескольких случайных аргументов.
Пусть Y=φ(X1, X2, …, Xn) и известна совместная плотность вида f(x1, x2,…, xn). Для расчётов используем формулы вида:
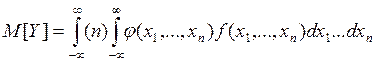 (6.2)
(6.2)
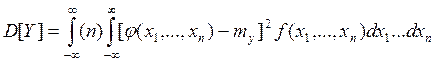 (6.3)
(6.3)
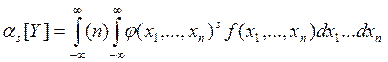 (6.4)
(6.4)
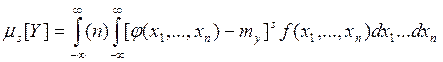 (6.5)
(6.5)
Очевидно, что с ростом размерности системы НСВ появляются сложности аналитического и вычислительного направлений.
Идею упрощения покажем на примере системы НСВ размерности 2.
Известно, что совместная плотность пары случайных величин X1 и X2, непрерывных по своей природе, выражается в общем виде как
![]() , где
, где
![]() - условная плотность СВ X1 при условии, что СВ X2
приняла значение x2.
- условная плотность СВ X1 при условии, что СВ X2
приняла значение x2.
Мы можем записать симметричную форму в виде
![]()
с той же интерпретацией.
Замечание. Это правило строго называют теоремой умножения плотностей (в схеме непрерывных случайных величин).
Если сейчас попытаться, например, оценить значение M[Y], где Y=φ(X1, X2), то необходимо использовать формулу
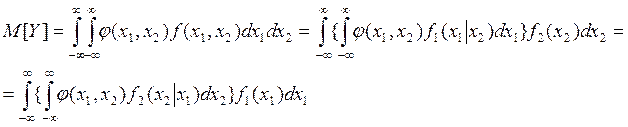 (6.6)
(6.6)
где внутренний интеграл представляет собой условное математическое ожидание, которое затем преобразуется в безусловное. Такое преобразование называют интегральной формулой полного математического ожидания.
Можно обобщить такую формулу на систему n>2 случайных величин. Например, формула (6.2) принимает вид:
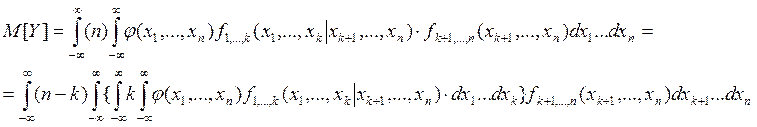 (6.7)
(6.7)
Эта формула построена как и (6.6), называется она интегральная формула полного математического ожидания для системы НСВ, заданных своей совместной плотностью f(x1,…,xn).
Запись формул для D[Y], αs[Y], μs[Y] в виде (6.7) требует только аккуратности.
Во многих прикладных задачах числовые характеристики СВ Y=φ(X1,…,Xn) можно определить как функции числовых характеристик системы СВ (X1,…,Xn). Главное – при этом нет необходимости знать законы распределения для системы, достаточно знать лишь числовые характеристики системы.
Перечислим именно такие случаи, (частично они нам знакомы).
M[c]=c
D[c]=0
M[cX]=cM[X] и D[cX]=c2D[X]
Для доказательства последнего следует представить D[cX] в виде
![]()
![]()
и его обобщение 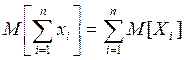
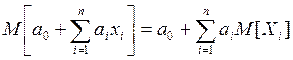
где ![]() ,
, ![]() - неслучайные величины.
- неслучайные величины.
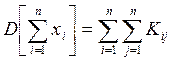
или, в силу симметрии матрицы ||Kij|| относительно главной диагонали, имеем
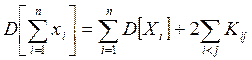
Замечание. Если СВ X1,…,Xn некоррелированы, т.е. Kij=0 при i≠j, то
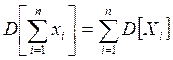
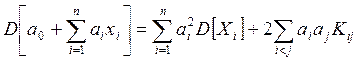
где a0,a1,…,an – неслучайные величины.
![]() , где
, где ![]()
Для некоррелированных СВ X1 и X2, т.е. при K12=0
![]()
Обобщение следует непосредственно при некоррелированности
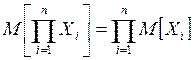
Оказывается, независимость системы упрощает все вычисления, т.к. независимость влечёт некоррелированность.
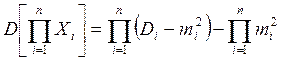
где Di=D[Xi], mi=M[Xi].
Напомним, что
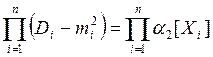
Y=aX+b, a и b – неслучайные величины
Имеем по определению
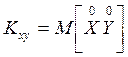
![]() . Тогда
. Тогда
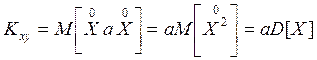 , что
и следовало ожидать.
, что
и следовало ожидать.
Для нормирования Kxy необходимо знать σy и σx.
![]() , т.е.
, т.е.
![]()
Тогда 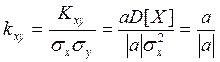 , т.е.
, т.е.
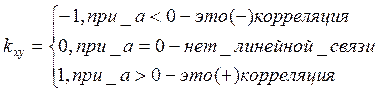
Таким образом, в общем случае
![]() -
это нам уже встречалось.
-
это нам уже встречалось.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.