Формула полной вероятности. Формула Байеса. Количество информации

ТемаЗ. Формула полной вероятности. Формула Байеса. Количество информации.

Рассматривается такой эксперимент со случайным исходом, точнее, исходами. Есть некоторое пространство элементарных исходов Ω. На нем может произойти n случайных событий, и мы предполагаем только их появления. Обозначать их будем H_i,

пусть i=1,n, т.е. n гипотез всего. Более того они взаимоисключающие.         Гипотезы         выдвигаются относительно формы проведения опыта, т.е. об условиях опыта можно сделать n исключающих друг друга предположений (гипотез). Каждая гипотеза осуществляется случайным образом.

Формально мы имеем:

Систему гипотез-событий,  причем  она  обладает полнотой,   H₁, H₂,…, H_n   и взаимоисключением, т.е. H_i • H_j =0, ij

Дополнительно рассматривается некоторое событие  А, причем появиться оно может только с одной из гипотез.

Задача заключается в определении вероятности Р(А)

Допустим, нам известны вероятности гипотез, т.е. Р(Н₁),Р(Н₂),...,Р(Н_n) и ясно, что 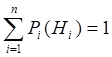 в силу полноты.

Пусть нам известны условные вероятности вида Р(А | Н₁ ),Р(А | H₂),...,P(A| H_n).

Мы   должны   принять,   что   система   вида   Н₁А, Н₂А,...,Н_пА   представляется

несовместной,   т.е.   появление   любого   произведения   вида   Н_i A, i =1, nисключает появление всех остальных.

Известно, что событие А  мы можем представить как сумму  п несовместных вариантов события А, т.е. на языке событий имеем А = Н₁А + Н₂А +... + Н_nА = ΣНiA

Далее   мы   можем   применить   правило   сложения   вероятностей, и   получить

Р(А) = ΣР(НiА).

Ясно, что события H_i   и  А   зависимы, тогда по теореме умножения имеем Р(Н_iА)=Р(Н_i)P(А|Н_i).

Окончательно для Р(А) имеем Р(А) = ΣP(H_i)P(A| Н_i)              (3.1)

Это и есть формула полной вероятности, позволяющая учесть гипотетические условия (гипотезы) для расчета безусловной вероятности события А.

Она позволяет формализовать случай, когда можно в опыте выделить два этапа:

_____ на первом - "разыгрываются" условия или форма опыта, что позволяет

оценить P(Н_i ) и выдвинуть гипотезы Н_i

на втором - "разыгрывается" результат нашего опыта.