Вероятное и достоверное. Понятие вероятности. Эмпирическая основа

Тема 1. Вероятное и достоверное. Понятие вероятности. Эмпирическая основа. Оценка вероятности. Определения и комментарии.

Мы все пользуемся словами "вероятный" и "достоверный" и, как правило, нет расхождения относительно их значения. Однако практика настоятельно и очень давно потребовала уточнить это значение в той мере, настолько это возможно.

Результат: вероятность - повседневное понятие. На это указывает ряд обычных слов, например, случай, наугад, риск, удача, шанс, неопределенность, верить, ожидать. Там где есть разнообразие, там всегда есть масса вероятностных проблем. Например, в сфере человеческой деятельности при построении социальных и приложение теории вероятностей - управление процессами или, в более общей ситуации, задачи принятия решений. В самой своя прелесть: она обладает внутренней структурой совершенно независимо от приложений.

Дальнейшая наша задача - численное уточнение качественных категорий: как и зовет Наука: числа... числа необходимы!

Теория вероятностей - наука, изучающая закономерности в случайных явлениях.

Определение 1.1 Случайное явление - это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Классическим примером такого рода является подбрасывание монеты: подбрасывание - это опыт (эксперимент), результат - выпадение герба или решки. Степень непредсказуемости, неопределенности здесь явная, хотя эксперимент простейший. Причина такого факта - невозможность учета множества связей. Теория вероятностей как раз пытается создать количественный базис для обсуждения ситуаций. Оказывается, что при огромном числе наблюдений случайного явления появляется некоторая закономерность.

Цель методов теории вероятностей - отказ от исследования отдельного явления с существенной неопределенностью в силу сложности и моделирование закономерностей массы таких явлений. Часто говорят, что теория вероятностей изучает закономерности в массовых случайных явлениях.

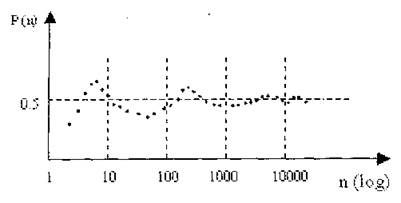
Необходимой отправной точкой может служить, например, следующее эмпирическое наблюдение. Предположим, что повторно подбрасывается монета, и каждый раз регистрируется число r(n) появлений герба в n первых подбрасываниях, n = 1,2,3,... Рассмотрим появления герба после n подбрасываний (или относительную частоту): P(n) = r(n) / n.                 (1.1)

Примерное поведение P(n) эмпирически установлено и в зависимости от n

показано на рисунке.