Цель работы: используя метод половинного деления, метод хорд и комбинированный метод
вычислить с точностью до ![]() действительные корни
уравнения третьего порядка
действительные корни
уравнения третьего порядка ![]() .
.
Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т.д.).
d0, d1, d2, d3- числовые коэффициенты исходного уравнения;
![]() - погрешность;
- погрешность;
h – шаг при отделении корней.
![]() - интервал для первого корня,
- интервал для первого корня, ![]() -приближённое значение первого корня,
-приближённое значение первого корня, ![]() - число итераций;
- число итераций;
![]() - интервал для второго корня,
- интервал для второго корня, ![]() -приближённое значение второго корня,
-приближённое значение второго корня, ![]() - число итераций;
- число итераций;
![]() - интервал для третьего корня,
- интервал для третьего корня, ![]() -приближённое значение третьего корня,
-приближённое значение третьего корня, ![]() - число итераций.
- число итераций.
1. постановку задачи;
2. блок-схему реализации используемого численного метода;
3. программу решения задачи.
При определении корня нелинейного уравнения выполняются два этапа:
- этап отделения корней;
- этап уточнения корней.
1. Отделение действительных корней.
Рассмотрим уравнение ![]() . Отделение корней методом
перебора (табличный метод) проводится на основании следующей теоремы:
. Отделение корней методом
перебора (табличный метод) проводится на основании следующей теоремы:
если непрерывная функция ![]() принимает значения
разных знаков на концах отрезка
принимает значения
разных знаков на концах отрезка ![]() , т.е.
, т.е. ![]() , то внутри этого отрезка находится, по
крайней мере, один корень уравнения
, то внутри этого отрезка находится, по
крайней мере, один корень уравнения ![]() .
.
На практике необходимо определить знаки функции ![]() в ряде точек х1, х2,
… из области определения функции. Если
в ряде точек х1, х2,
… из области определения функции. Если ![]() , то в
силу приведенной выше теоремы на отрезке
, то в
силу приведенной выше теоремы на отрезке ![]() имеется,
по крайней мере, один корень уравнения
имеется,
по крайней мере, один корень уравнения ![]() .
Необходимо проверить, является ли этот корень единственным. Если на отрезке
.
Необходимо проверить, является ли этот корень единственным. Если на отрезке ![]()
![]() не меняет знак, корень
– единственный (в силу монотонности
не меняет знак, корень
– единственный (в силу монотонности ![]() ).
).
Пусть найден отрезок ![]() , содержащий
единственный корень уравнения
, содержащий
единственный корень уравнения ![]() , который обозначим
через
, который обозначим
через ![]() . Для нахождения корня уравнения делим
отрезок
. Для нахождения корня уравнения делим
отрезок ![]() пополам.
пополам.
Если 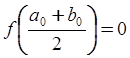 , то
, то 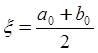 и задача решена.
и задача решена.
Если 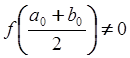 , то выбираем ту из половин
отрезка, на концах которой функция
, то выбираем ту из половин
отрезка, на концах которой функция ![]() имеет противоположные
знаки. Новый суженный отрезок
имеет противоположные
знаки. Новый суженный отрезок ![]() снова делим пополам и
повторяем те же рассуждения и т.д. В результате, на каком то этапе получаем или
точный корень уравнения или последовательность вложенных друг в друга отрезков
снова делим пополам и
повторяем те же рассуждения и т.д. В результате, на каком то этапе получаем или
точный корень уравнения или последовательность вложенных друг в друга отрезков ![]() ,
, ![]() , …,
, …, ![]() , … .
, … .
Если необходимо вычислить корень уравнения с точностью до ![]() , деление отрезка
, деление отрезка ![]() производится
до тех пор, пока выполняется условие
производится
до тех пор, пока выполняется условие ![]() . За приближенное
значение корня берется средняя точка отрезка
. За приближенное
значение корня берется средняя точка отрезка ![]() .
.
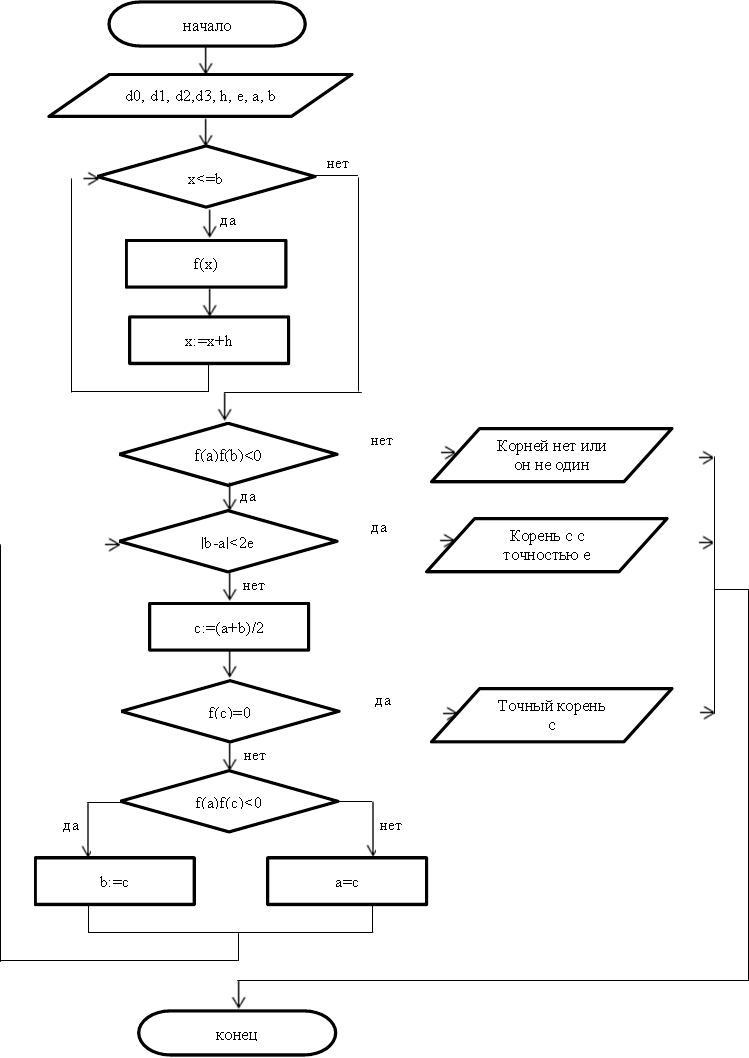
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Grids, Menus;
type
TForm1 = class(TForm)
Edit1: TEdit;
Label1: TLabel;
Edit2: TEdit;
Label2: TLabel;
Edit3: TEdit;
Label3: TLabel;
Edit4: TEdit;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Edit5: TEdit;
Label7: TLabel;
Label8: TLabel;
Edit7: TEdit;
Label9: TLabel;
Edit8: TEdit;
Label10: TLabel;
Edit6: TEdit;
Label11: TLabel;
Button1: TButton;
StringGrid1: TStringGrid;
Label12: TLabel;
Label13: TLabel;
StringGrid2: TStringGrid;
MainMenu1: TMainMenu;
N1: TMenuItem;
N2: TMenuItem;
N3: TMenuItem;
N4: TMenuItem;
N5: TMenuItem;
procedure Button1Click(Sender: TObject);
procedure N5Click(Sender: TObject);
procedure N2Click(Sender: TObject);
procedure N3Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
d3,d2,d1,d0,e,h,a,b,x,f,c:real;
implementation
uses unit2, unit3;
{$R *.dfm}
function y(x:real):real;
begin
y:=d3*x*x*x+d2*x*x+d1*x+d0;
end;
procedure TForm1.Button1Click(Sender: TObject);
var i,j:integer;
begin
d3:=strtofloat(Edit1.Text);
d2:=strtofloat(Edit2.Text);
d1:=strtofloat(Edit3.Text);
d0:=strtofloat(Edit4.Text);
e:=strtofloat(Edit5.Text);
h:=strtofloat(Edit6.Text);
a:=strtofloat(Edit7.Text);
b:=strtofloat(Edit8.Text);
x:=a;
i:=0;
j:=0;
StringGrid1.Cols[0].Clear;
StringGrid1.Cols[1].Clear;
StringGrid2.Cols[0].Clear;
label12.Caption:='';
label13.Caption:='';
StringGrid1.Cells[0,0]:='x';
StringGrid1.Cells[1,0]:='f(x)';
StringGrid2.Cells[0,0]:='f(a)';
while x<=b do
begin
f:=y(x);
i:=i+1;
StringGrid1.RowCount:= StringGrid1.RowCount+1 ;
StringGrid1.Cells[0,i]:=Floattostr(x);
StringGrid1.Cells[1,i]:=Floattostr(f);
x:=x+h;
end;
if y(a)*y(b)<0 then
begin
repeat
StringGrid2.RowCount:= StringGrid2.RowCount+1 ;
StringGrid2.Cells[0,0]:='Интервал';
c:=(a+b)/2 ;
if y(c)=0 then
begin
label12.Caption:='Точный корень: '+floattostr(c);
exit;
end
else
if y(a)*y(c)<0 then
begin
StringGrid2.Cells[0,j+1]:='[ '+Floattostr(a)+' ; '+Floattostr(b)+' ]';
j:=j+1;
b:=c ;
end
else
begin
StringGrid2.Cells[0,j+1]:='[ '+Floattostr(a)+' ; '+Floattostr(b)+' ]';
j:=j+1;
a:=c;
end;
until (abs(b-a)<2*e);
label13.Caption:='Корень с точностью '+ floattostr(e)+' равен '+floattostr(c);
end
else
label13.Caption:='Корня нет или он не один';
end;
procedure TForm1.N2Click(Sender: TObject);
begin
form2.ShowModal;
end;
procedure TForm1.N3Click(Sender: TObject);
begin
form3.ShowModal;
end;
procedure TForm1.N5Click(Sender: TObject);
begin
if messagedlg ('Работа окончена?', mtConfirmation,[mbYes,mbNo],0)=mrYes then
close;
end;
end.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.