Абсолютная погрешность суммы чисел равна сумме абсолютных погрешностей слагаемых.
Относительная погрешность суммы этих чисел dS заключается между наибольшей и наименьшей из относительных погрешностей слагаемых. То есть она не превышает наибольшей из относительных погрешностей слагаемых.
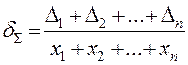 (1.6)
(1.6)
С другой стороны имеем равенства:
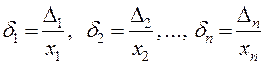 , (1.7)
, (1.7)
а так как все дроби (1.6) рассматриваются лишь по их численной величине, то дробь (1.6), представляющая отношение суммы числителей к сумме знаменателей, заключается между наибольшей и наименьшей из дробей (1.7).
Поэтому, в том случае, когда все слагаемые приблизительно одинаковой величины (отношение наибольшего из них к наименьшему менее 10 [1]), надо их писать с одним и тем же числом знаков, столько же верных знаков будет и в сумме.
Если числа сильно разнятся по величине, то разрядность их уравнивают по разрядности наибольшего из чисел. Однако в этом случае необходимо иметь информацию о том, как получены эти значения и не является ли число, резко отличающееся от остальных, например, "грубым выбросом", ошибочным значением и т.д. Тогда ориентироваться на него надо осторожно или вовсе этого не делать.
Пример. Сложить числа: 2,374; 2,8232; 0,52181; 0,014253, тогда не следует делать сложение так показано в п. а), а следует делать так, как показано в п. б):
|
а) 2,374 + 2,8232 0,52181 0,014253 5,733263 |
б) 2,374 + 2,823 0,522 0,014 5,733 |
При сложении приближённых чисел абсолютная погрешность может быть как положительной, так и отрицательной, при этом может происходить взаимная компенсация погрешностей.
Погрешность произведения. Относительная погрешность произведения чисел равна сумме относительных погрешностей слагаемых.
Пусть множители х1, х2 имеют относительные погрешности d1, d2. Следовательно, истинные величины этих чисел можно представить:
х1 = х1 (1 + d1) и х2 = х2 (1 + d2) (1.8)
Истинная величина произведения будет:
х1 х2 = х1 х2 (1 + d1)(1 + d2) = х1 х2(1 + (d1 + d2) + d1d2) (1.9)
Обыкновенно d1 и d2 весьма малы, например, 0,001; тогда произведение d1d2 будет весьма мало по сравнению с их суммой и эти произведением можно пренебречь. Тогда имеем:
х1 х2 = х1 х2(1 + (d1 + d2)) = х1 х2 + х1 х2(d1 + d2), (1.10)
что подтверждает высказанное свойство для случая двух множителей, которое распространяется и на любое их количество.
Деление. Так как деление на число х
равносильно умножению на число ![]() , то при делении
относительная погрешность частного равна сумме относительных погрешностей
делимого и делителя. Этой величины она достигает при условии, когда абсолютные
погрешности делимого и делителя разных знаков.
, то при делении
относительная погрешность частного равна сумме относительных погрешностей
делимого и делителя. Этой величины она достигает при условии, когда абсолютные
погрешности делимого и делителя разных знаков.
Возведение в степень. Относительная погрешность m-ой степени числа равна m-кратной относительной погрешности этого числа. Относительная погрешность квадрата числа равна удвоенной относительной погрешности числа, куба – утроенной и т.д. Относительная погрешность корня m-ой степени числа составляет 1/m часть относительной погрешности числа.
То есть это справедливо и для дробных степеней:
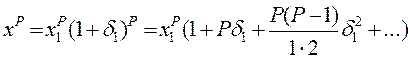 , (1.11)
, (1.11)
где Р - степень числа.
Поскольку d мала, то всеми членами, её содержащими можно пренебречь, тогда:
![]() (1.12)
(1.12)
Вычитание. Относительная погрешность разности не поддаётся простому учёту. Особенно не благоприятна в этом смысле разность двух близких по величине чисел.
Например, пусть даны числа: 52,287 и 51,939. Разность
между ними равна 0,348. Как известно, в каждом из исходных чисел можно ручаться
только за первые четыре цифры, а так как в последней погрешность не более 1, то
относительная погрешность самих чисел не более ![]() . Между
тем как в разности этих чисел 0,348 последняя цифра может быть неверна уже на
две единицы и относительная погрешность может составить
. Между
тем как в разности этих чисел 0,348 последняя цифра может быть неверна уже на
две единицы и относительная погрешность может составить ![]() ,
т.е. примерно в триста раз большую величину нежели в данных.
,
т.е. примерно в триста раз большую величину нежели в данных.
Относительная погрешность разности во столько же раз больше относительной погрешности в слагаемых, во сколько раз сама разность меньше каждого из них.
Представим сводку тех общих правил, которые вытекают из приведённых
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.