Операционные усилители. Усилители на АУ. Дифференциальные усилители на АУ. Измерительные усилители. Моменты случайных величин, страница 6

Сігналы падзяляюцца на дэтэрмінаваныя і выпадковыя (стахастычныя). Дэтэрмінаванымі з’яўляюцца сігналы, якія вызначаны ў любы момант часу. Сігнал s(t) = Am sin(wt + j) детэрмінаваны пры вядомых Am, w, j. Выпадковымі з’яўляюцца сігналы, дакладнае значэнне якіх у любы момант часу вызначыць немагчыма, іх апісваюць выпадковымі функцыямі. Выпадковая функцыя x(t) – гэта функцыя, якая ў любы момант часу з’яўляецца выпадковай велічынёй. Выпадковай з’яўляецца велічыня, якая ў выніку доследу прымае адно, загадзя невядомае значэнне з мноства магчымых. Для характарыстыкі выпадковай велічыні неабходна задаць мноства яе магчымых значэнняў і імавернасць іх з’яўлення. Энергетычныя характарыстыкі сігналаў

Пад энергіяй сігналу u(t) разумеюць велічыню

.

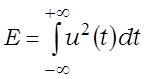Калі сігнал мае канечную працягласць T (не роўны нулю на адрэзку часу [–T/2, T/2]), то яго энергія вызначаецца як

.

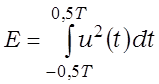З выкарыстаннем (1.17) выраз для энергіі набывае выгляд

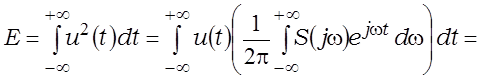
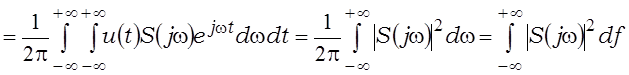, дзе úS(jw)ç² – спектральная шчыльнасць энергіі, якая вызначаецца з выразаў

;

.

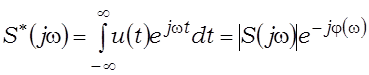Атрыманая роўнасць з’яўляецца роўнасцю Парсеваля. Яна вызначае энергію сігналу праз часавую функцыю ці спектральную шчыльнасць энергіі.

Разгледзім сігнал, які існуе на абмежаваным інтэрвале [–T/2, T/2]. Да такога сігналу можна прымяніць роўнасць Парсеваля. Тады

.

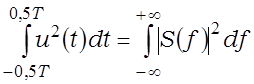Падзелім левую і правую часткі роўнасці на час T і накіруем апошні ў бясконцасць:

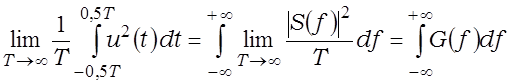, дзе велічыню

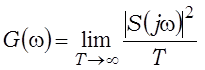
называюць спектральнай шчыльнасцю магутнасці. З павелічэннем T энергія і úS(jw)ç² незатухальных ваганняў узрастаюць, аднак іх адносіна можа імкнуцца да акрэсленай мяжы, якая з’яўляецца спектральнай шчыльнасцю магутнасці G(w).

Пры аналізе электрычных схем выкарыстоўваюць паняцці імгненнай магутнасці, сярэдняй магутнасці сігналу і (як асобны выпадак) сярэдняй магутнасці перыядычнага сігналу, якія магчыма разлічыць наступным чынам:

; ; .

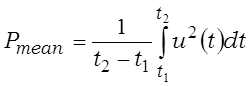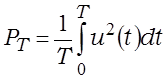Паласой частот сігналу называюць тую частку спектра, дзе сканцэнтравана 90¸95% яго магутнасці.

2Моменты случайных величин

Бесперапынная выпадковая велічыня прымае адвольнае значэнне з некаторага інтэрвалу. Яе імавернаснай характарыстыкай з’яўляецца функцыя размеркавання F(x), якая дае імавернасць таго, што значэнне выпадковай велічыні X меншае за лік x. Функцыя размеркавання дазваляе вызначыць імавернасць таго, што выпадковая велічыня X трапіць у інтэрвал [a,b]: P(a £ x £ b) = F(b) – F(a). Шчыльнасцю імавернасці, ці дыферэнцыяльным законам размеркавання выпадковай велічыні, з’яўляецца функцыя p(x) = dF(x)/dx . Тады p(x)dx дае імавернасць пападання Х у інтэрвал [x, x + dx]. Імавернасць пападання выпадковай велічыні X у інтэрвал [a,b]

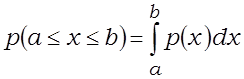. Тады .

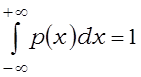Момант выпадковай велічыні парадку k вызначаецца як

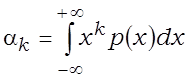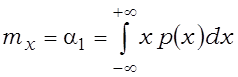;           , дзе a₁ – першы момант выпадковай велічыні, які называецца матэматычным чаканнем. Спрошчана лічаць матэматычнае чаканне сярэднім значэннем. Цэнтральным (цэнтраваным) момантам выпадковай велічыні парадку k называюць

.

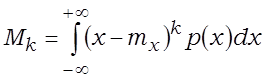Цэнтральны момант другога парадку называецца дысперсіяй:

.

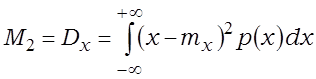Яна характарызуе роскід значэнняў выпадковай велічыні вакол матэматычнага чакання (сярэдняга значэння). Сярэднеквадратычнае адхіленне вызначаецца ў выглядзе sx = , сярэднеквадратычнае значэнне

.

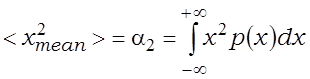Найбольш часта сустракаецца нармальны закон размеркавання шчыльнасці імавернасці

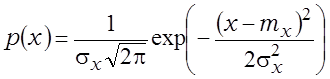.           (1.1)

Імавернасць пападання нармальна размеркаванай велічыні x у інтэрвал [a,b] вызначаецца ў выглядзе

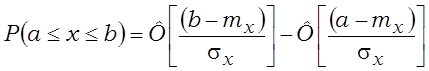,        (1.2)

дзе Ф – інтэграл Кашы (інтэграл памылак),

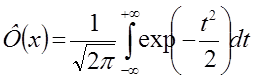
На рисунке 1.1 выпадковыя велічыні X і Y, якія разглядаюцца разам, прымаюць як выпадковы пункт на плоскасці OXY ці выпадковы вектар з пачатку каардынат у пункт з каардынатамі [x,y]. Функцыяй размеркавання ці інтэгральным законам размеркавання сістэмы выпадковых велічынь Х і Y называюць імавернасць сумеснага выканання F(x,y) = = P [(X < x),(Y < y)]. Тады P [(a £ X £ b),c £ Y £ d)] = = F(b,d) – F(b,c) – F(a,d) + F(a,c).