Операционные усилители. Усилители на АУ. Дифференциальные усилители на АУ. Измерительные усилители. Моменты случайных величин, страница 4

Работа інтэгратара з папярэдняй ненулявой устаноўкай узроўню выхадного напружання адрозніваецца ад разгледжанай тым, што перад пачаткам інтэгравання SA2 і SA3 замкнуты, SA1 разамкнуты, таму схема з’яўляецца інверсавальным узмацняльнікам, на ўваход якога паступае u0. Імгненнае значэнне выхаднога напружання ў час інтэгравання мае выгляд

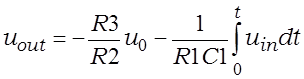.                        (3.15)

Ключы на мал. 3.3 выконваюць на транзістарах.

12Дифференциаторы

Схемы інтэгратара і дыферэнцыятара на АУ прыведзены на мал. 3.1. Правядзём разлік перадатачных характарыстык і сувязі выхаднога напружання з уваходным у часавай вобласці. Для гэтага складзём ураўненні паводле другога закону Кірхгофа па контурах: 1) ^, uin, C1, «–» уваход, «+» уваход, ^; 2) ^, «+» уваход, «–» уваход, R1, выхад, uout, ^ для дыферэнцыятара, да якіх далучым ураўненне паводле першага закону Кірхгофа для інверсавальнага ўвахода для дыферэнцыятара. Вывад сувязі выхаднога напружання з уваходным у часавай вобласці патрабуе скласці гэтыя ўраўненні для імгненных значэнняў, вывад перадатачных характарыстык – для адлюстраванняў па Лапласу. Пры запісе ўраўненняў адразу ўлічым якасць ідэальнага АУ.

Для дыферэнцыятара сістэма ўраўненняў у часавай вобласці

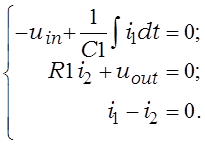          (3.3)

З (3.3) атрымліваем сувязь выхаднога напружання з уваходным у часавай вобласці для дыферэнцыятара:

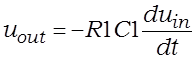.                                   (3.4)

З (3.2) і (3.4) выцякае, што інтэгратар інтэгруе, а дыферэнцыятар дыферэнцуе ўваходны сігнал з каэфіцыентам, які залежыць ад пастаяннай часу RC-ланцуга.

Для дыферэнцыятара аналагам (3.3) у вобласці адлюстраванняў па Лапласу з’яўляецца сістэма

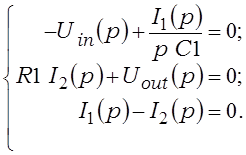                               (3.7)

З (3.7) выцякае выраз для перадатачнай характарыстыкі дыферэнцыятара

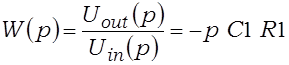.                           (3.8)

Каэфіцыенты перадачы дыферэнцыятара адпаведна

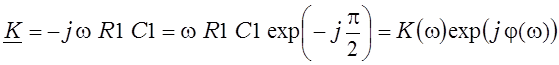.  (3.10)

амплітудна-частотная (АЧХ) і фазава-частотная (ФЧХ) характарыстыкі інтэгратара і дыферэнцыятара маюць выгляд

; .

У сувязі з тым што дыферэнцыятар валодае вялікім каэфіцыентам узмацнення на адносна высокіх частотах і мае ўласнае зрушэнне фазы –90°, то пры наяўнасці ў схеме дадатковых ланцугоў, якія затрымліваюць фазу на 90°, для дыферэнцыятара адмоўная зваротная сувязь пераўтвараецца ў дадатную, а сама схема – у генератар. З-за няўстойлівасці стандартнай схемы на практыцы ў дыферэнцыятарах абмяжоўваюць каэфіцыент узмацнення на ўсіх частотах альбо толькі на высокіх пры дапамозе рэзістара, паслядоўна злучанага з кандэнсатарам, ці пры дапамозе кандэнсатара, паралельна злучанага з рэзістарам (мал. 3.5).

Перадатачныя характарыстыкі дыферэнцыятараў на мал. 3.5 маюць выгляд

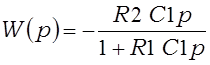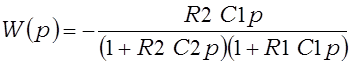; . (3.18)

13 Сумматоры

Для разліку схемы суматара ў сістэме (2.6) заменім ураўненне паводле першага закону Кірхгофа для вузла каля інверсавальнага ўвахода. Дапоўнім яе ўраўненнем паводле другога закону Кірхгофа па контуры ^, uin₂, R4, «–» уваход, «+» уваход, R3, ^; прымем, што ў якасці uin выступае uin₁ (uin = uin₁), а АУ з'яўляецца ідэальным (уваходныя токі роўны 0 і DU = 0):

;.                       (2.10)

Тады з (2.6) з улікам (2.10) для суматара атрымаем

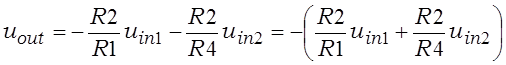.       (2.11)

Пры неабходнасці мець больш за два падсумавальныя ўваходы інверсавальны ўваход АУ злучаюць з крыніцамі напружання праз дадатковыя рэзістары па аналогіі з R4. R3, як і ў схемах узмацняльнікаў, забяспечвае кампенсацыю ўваходных токаў. Яго велічыня выбіраецца як эквівалентнае супраціўленне паралельна злучаных R1, R2, R4. Суматар мае рознае супраціўленне па падсумавальных уваходах: па uin₂ Rin₂ = R4; па uin₁ Rin₁ = R1.