|
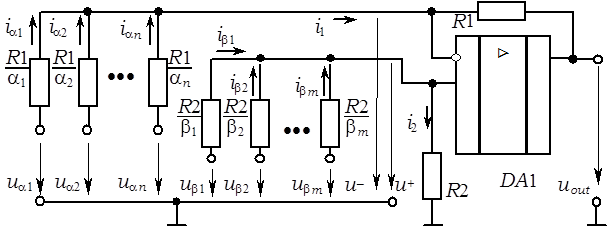
Мал. 2.7. Прынцыповыя схемы дыферэнцыяльнага ўзмацняльніка (а) і суматара (б) |
Для вываду выхаднога напружання універсальнай схемы падсумавання-адымання складзём ураўненні паводле другога закону Кірхгофа па контурах: 1) ^, ub1, R2/b1, «+» уваход, R2, ^; 2) ^, ub2, R2/b2, «+» уваход, R2, ^; …; m) ^, ubm, R2/bm, «+» уваход, R2, ^ і ўраўненне паводле першага закону Кірхгофа для «+» увахода:
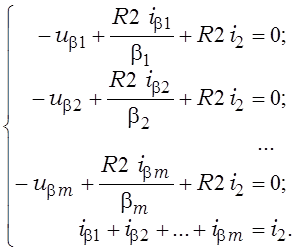 (2.15)
(2.15)
Знаходзячы з (2.15) ток i2, выражаем u+ = R2 i2 і з улікам u+ = u– складаем ураўненні паводле другога закону Кірхгофа па контурах: 1) ^, ua1, R1/a1, «–» уваход, «+» уваход, u+, ^; 2) ^, ua2, R1/a2, «–» уваход, «+» уваход, u+, ^; …; n) ^, uan, R1/am, «–» уваход, «+» уваход, u+, ^; n + 1) ^, u+, «+» уваход, «–» уваход, R1, uout, ^ і ўраўненне паводле першага закону Кірхгофа для інверсавальнага ўвахода:
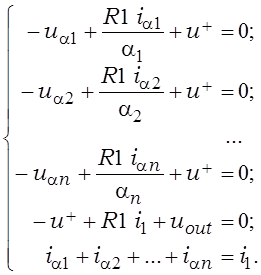 (2.16)
(2.16)
З сістэмы (2.16) атрымаем канчатковую формулу
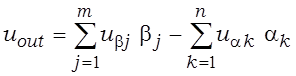 . (2.17)
. (2.17)
14Пассивные фильтры
Гэтыя фільтры называюць таксама інтэгравальнымі і дыферэнцавальнымі ланцугамі. Сэнс назвы заключаецца ў тым, што ланцугі пры пэўных умовах інтэгруюць ці дыферэнцуюць уваходны сігнал, а пры іншых – прапускаюць яго без змянення. Разгляд работы фільтраў зробім пры ўмове бясконца вялікага супраціўлення нагрузкі і роўнага нулю ўнутранага супраціўлення крыніцы, якая стварае ўваходнае напружанне. З ураўненняў паводле другога закону Кірхгофа па контуры ^, uin, R1, C1, ^ знаходзім перадатачныя характарыстыкі ФНЧ (Wi) і ФВЧ (Wd) на R- і C- элементах:
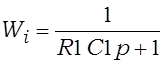 ,
, 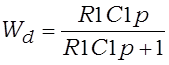 . (3.19)
. (3.19)
Камплексныя каэфіцыенты перадачы гэтых ланцугоў
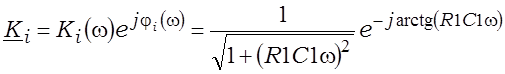 ; (3.20)
; (3.20)
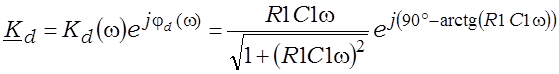 (3.21)
(3.21)
|
Мал. 3.6. Прынцыповыя схемы ФНЧ (фільтраў нізкіх частот), інтэгравальных ланцугоў (а) і ФВЧ (фільтраў высокіх частот), дыферэнцавальных ланцугоў (б) |
надаюць АЧХ, ФЧХ і АФЧХ выгляд, які адлюстраваны на мал. 3.7. Характэрнай для ФНЧ і ФВЧ з’яўляецца частата w0, пры якой узровень K(w) складае 1/ »0,71 ад максімальнага значэння. Яе называюць частатой зрэзу.
Пераходзячы ад перадатачнай характарыстыкі да функцый часу, атрымліваем для інтэгравальнага ланцуга
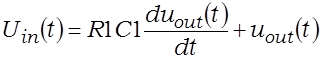 . (3.22)
. (3.22)
Пры выкананні ўмовы R1C1duout(t)/dt << uout(t) можна пагрэбаваць першым складаемым у (3.22), і uout » uin. Сігналы, для якіх выконваецца апошняя няроўнасць, называюць маруднымі. Сігналы, для якіх выконваецца R1C1duout(t)/dt >> uout(t), называюць хуткімі, і ў гэтым выпадку
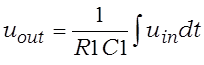 .
.
Такім чынам, інтэгравальны ланцуг інтэгруе хуткія сігналы і прапускае без змянення марудныя. Аналагічна дыферэнцавальны ланцуг прапускае без змянення хуткія і дыферэнцуе марудныя сігналы.
Для моста Віна (рэжэктарны фільтр на мал. 3.8б) вывад перадатачнай характарыстыкі і камплекснага каэфіцыента перадачы патрабуе дадаткова выкарыстаць ураўненне
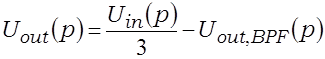 ,
,
|
Мал. 3.8. Паласавыя і рэжэктарныя пасіўныя фільтры: а) паласавы фільтр на R і C; б) мост Віна – рэжэктарны фільтр; в) паласавы фільтр на паралельным вагальным контуры; г) рэжэктарны фільтр на паралельным вагальным контуры (фільтр-пробка); д) паласавы фільтр на паслядоўным вагальным контуры; е) рэжэктарны фільтр на паслядоўным вагальным контуры; ж) двайны Т-падобны рэжэктарны фільтр |
Вывад перадатачнай характарыстыкі двайнога Т-падобнага рэжэктарнага фільтра патрабуе пераўтварэння зоркі ў трохвугольнік, таму прасцей правесці разлік пры дапамозе метаду вузлавых патэнцыялаў для адлюстраванняў па Лапласу, дзеля чаго патрэбна запісаць сістэму ўраўненняў для вузлоў 1, 2 і 3 на мал. 3.8ж. З гэтай сістэмы знаходзім перадатачную характарыстыку ў выглядзе
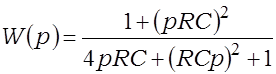 ; (3.35)
; (3.35)
1Сигналы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.