Построение переходных процессов для линейных дискретных систем. Передаточные функции противоточного КТТ без учета накопления тепла в стенке. Деформационные манометры

ТАУ 11. Построение переходных процессов для линейных дискретных систем.

Рассмотрим импульсную передаточную функцию звена или системы. Пусть мы имеем звено, кот. описывается в форме передаточной ф-и или в форме весовой ф-и.

Вводим квантователь на входе и выходе системы. Для простоты, считаем что квантователи синхронизированы. U(t) – входной сигнал и если квантователи идеальны, то на выходе мы имеем

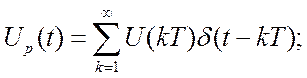
y(t) –выход звена:

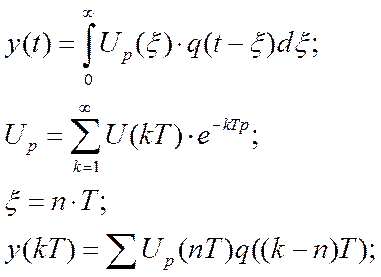
Если сделать некоторые преобразования и произвести ряд замен, то получим:

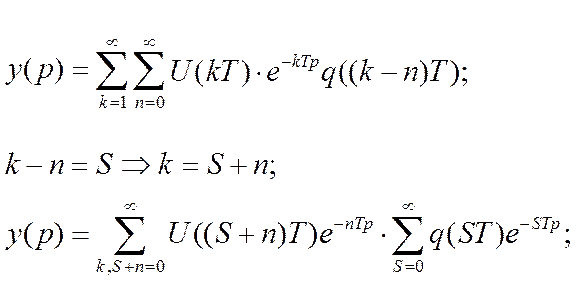
в результате получили две отдельные суммы. Если сделать подстановку

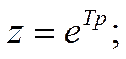
получим      

       

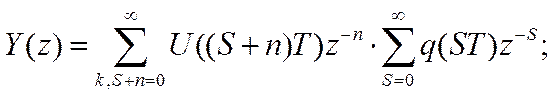
последняя часть выражения и будет импульсной передаточной ф-ей W(z).

Имеем такую же форму как и для преобразования Лапласа. W(z) – импульсная передаточная ф-я, её можно получить на основе весовой ф-и или на основе z-преобразования         

МОД 11-1. Передаточные функции противоточного КТТ

без учета накопления тепла в стенке

Математическая модель:

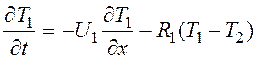
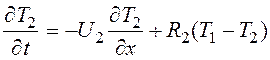
Нач.усл.:                                          

Гран.усл.:                                 

Уравнения можно преобразовать по Лапласу только по времени ,по линейной координате нельзя, т.к. они имеют различные гран. условия.

Преобразуем   при нулевых нач. условиях:

         

         

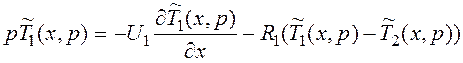
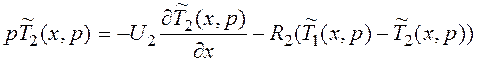
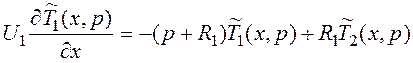
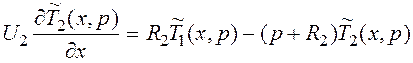
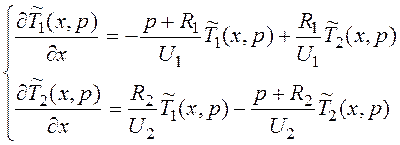
Запишем эту систему в матричной форме: . Для решения надо составить характеристическое уравнение:

      

  

 ;    

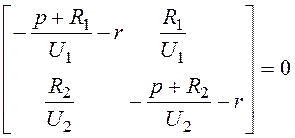
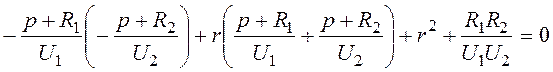
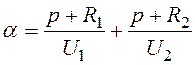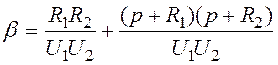
Можно найти корни ХАУ и при этих корнях решения системы системы уравнений:

                             -постоянные интегрирования, которые

                              находятся из гран. условий.

Продифференцируем по линейной координате:

МОД 11-2

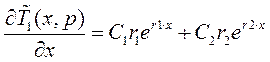
Обозначим 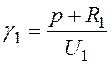   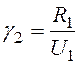; , тогда получим:

 :                           

:                         

Рассмотрим 1-ое граничное условие в уравнении:

         

             

Умножим на :

Умножим     на :

Левые части последних двух уравнений равны    равны и правые:

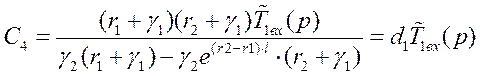
Тогда 

Получим:

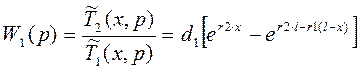
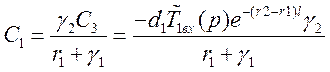
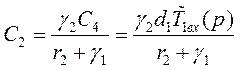
Получим:

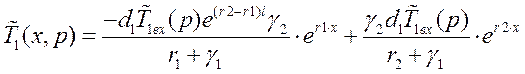
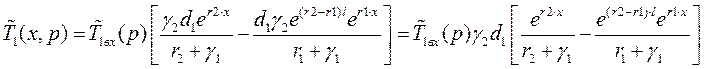
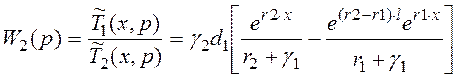
АЭП 11-1. ДПТ как объект системы автоматического управления

Характер переходного процесса в системе автоматического управления зависит от динамических свойств элементов, из которых она состоит. Эти элементы могут выполняться виде машин, аппаратов, приборов и устройств различного действия( механического, электрического, пневматического, гидравлического и т. д.). Однако все эти элементы подразделяются на ограниченное число звеньев, обладающих одинаковыми динамическими свойствами и называемых типовыми динамическими звеньями.

В зависимости от характера протекания переходных процессов при единичных ступенчатых  воздействиях типовые динамические звенья делятся на безинерционные, апериодические, колебательные, дифференцирующие, интегрирующие, запаздывающие.

ДПТ можно отнести к инерционному звену 2-го порядка(в данном случае можно сказать, что двигатель- электромеханический элемент, способный запасать кинетическую энергию в якоре и электромагнитную в якорной цепи).

Инерционным звеном 2-го порядка  (или иначе, двухемкостным, апериодическим звеном 2-го порядка, колебательным) наз. звено, выходная величина которого при подаче на вход ступенчатого воздействия стремится к установившемуся значению, совершая затухающие колебания либо апериодически(монотонно) приближаясь к нему. Переходной процесс такого звена описывается ДУ 2-го порядка:

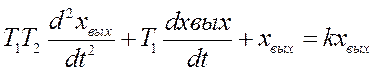 ,где ,-постоянные, имеющие размерность времени; k-коэфициент усиления звена.

Операторное изображение этого уравнения при нулевых начальных условиях слева имеет вид:

Вид переходного процесса определяется корнями ХАУ, которые зависят от соотношения постоянных времени  и , и может носить апериодический либо колебательный характер.

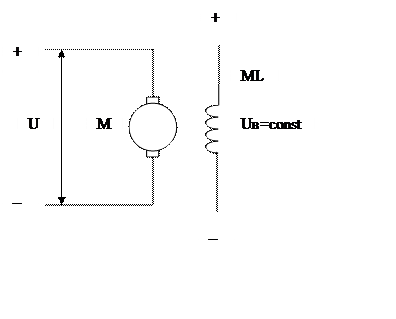       Входным воздействием ДПТ, работающего при постоянном магнитном потоке, является напряжение на якоре, а выходной координатой- угловая скорость . Если приложить к якорю двигателя воздействие в виде скачка напряжения, возникнет переходной процесс, который описывается ДУ:

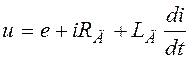       (1)

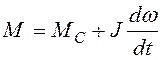            (2)

Выражение (1) представляет уравнение ЭДС главной цепи, а (2)- уравнение