Синтез дискретной системы управления непрерывным технологическим объектом

Учреждение образования

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет Заочный

Кафедра АТПиЭ

Специальность 1-53-01-01

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

 КУРСОВОГО ПРОЕКТА

по дисциплине «Теория автоматического управления»

Тема: «Синтез дискретной системы управления»

Исполнитель студент 5 курс                             ________________     Меленченок Е. А

подпись, дата

Руководитель

________________     Кузьмицкий И.Ф.

подпись, дата

Курсовой проект защищен с оценкой ______________

Руководитель_________________                                                         Кузьмицкий И.Ф.

подпись

Минск 2010

Содержание

Введение. 3

1       Переход от непрерывной к дискретной модели системы.. 4

2       Синтез дискретного апериодического регулятора. 8

3       Расчет дискретного компенсатора. 12

4       Аналитическое конструирование регулятора. 15

5       Синтез наблюдателя переменных состояния. 21

Заключение. 25

Список использованной литературы.. 26

Структура, результаты расчета дискретной системы управления. 27

Структура, результаты моделирования оптимальной системы управления. 28

Структура, результаты моделирования работы наблюдателя переменных состояния. 30

Введение

Импульсные автоматические системы в отличие от непрерывных систем работают на импульсных сигналах определённой периодичности. Импульсы характеризуются периодом повторения (цикла), высотой импульса, длительностью, полярностью и моментом начала импульса. Импульсные системы обычно представляют соединение импульсного элемента и некоторой непрерывной части. Устройство, формирующее последовательность импульсов, определяемую непрерывным входным сигналом, называется импульсным элементом.

Импульсные системы могут быть как линейные, так и нелинейные.

Динамику импульсной автоматической системы можно рассматривать в виде реакции непрерывной части системы на серию импульсов, чередующихся с заданным периодом. Конечные значения переменных для предыдущего цикла являются начальными для последующего цикла и т. д. Зная закон изменения внешнего воздействия, приведённого к входу импульсного элемента можно определить форму импульсов, поступающих на вход непрерывной части системы, и рассчитать переходной процесс на всём промежутке регулирования. Однако этот метод не позволяет исследовать устойчивость системы в целом и оценить влияние параметров на динамику системы.

Для устранения указанного недостатка было предложено контролировать процесс регулирования не непрерывно во времени, а дискретно один раз за период, например, в момент начала каждого цикла. В связи с этим в работах Жуковского и Хорта для исследования импульсных систем регулирования был применён аппарат дифференциально-разностных преобразований Лапласа и частотный метод, позволяющий применять известные в линейной теории методы анализа.

Преобразование непрерывного сигнала в дискретный называется квантованием сигнала. Существуют три вида квантования:

1) по уровню;

2) по времени;

3) по уровню и по времени.

Дискретные системы, соответствующие каждому из способов квантования, получили наименования релейных, импульсных и  цифровых систем автоматического управления.

В данном курсовом проекте будет рассмотрен синтез дискретной системы управления непрерывным технологическим объектом, а приведено аналитическое конструирование оптимального регулятора для данного объекта.

Целью курсового проекта является освоение методов анализа, синтеза и компьютерной имитации дискретных систем управления, освоение алгоритмов аналитического конструирования регуляторов и наблюдателя переменных состояния объекта.

1   Переход от непрерывной к дискретной модели системы

Каждая система управления, в которой присутствует хотя бы один элемент, который не подчиняется непрерывному характеру изменения сигнала, может быть отнесен к классу дискретных систем. Для этих систем характерным является исчезновения сигнала информации хотя бы на небольшом интервале времени. Если эти интервалы  устремить к нулю, то можно рассматривать систему как непрерывную. Дискретные системы более общие. В производстве часто технологические процессы непрерывные.

Дискретность (и, следовательно, разрывность) сигналов обусловлена их квантованием по уровню и (или) по времени. В противоположность непрерывным сигналам, которые описываются непрерывными функциями времени, дискретные сигналы могут принимать лишь дискретные значения в дискретные моменты времени. Обычно дискретный сигнал получается в результате периодического прерывания непрерывного сигнала с постоянным тактом. Существуют разные способы модуляции отдельных импульсов, входящих в последовательность. Они отличаются допустимыми значениями амплитуд, шириной импульсов и модулирующей частотой. В цифровых системах управления обычно применяется лишь амплитудная модуляция импульсов, причем в основном тот ее вариант, при котором высота импульса пропорциональна текущему значению непрерывного сигнала, ширина постоянна, а интервалы между импульсами одинаковы и равны такту квантования. Поскольку к дискретным сигналам этого типа применима теорема суперпозиции, они описываются линейными соотношениями, аналогичными по форме уравнениям линейных динамических систем.

Рассматриваемая система имеет вид, представленный на рисунке 1.1:

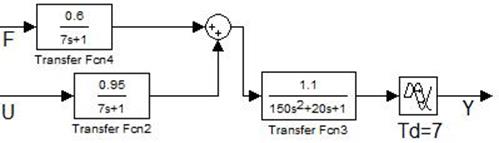
Рисунок 1.1- заданный объект с внешним воздействием

Без учета внешнего воздействия F система приобретёт вид, представленный на рисунке 1.2:

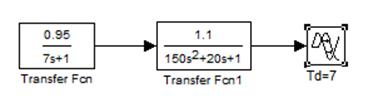
Рисунок 1.2 - заданный объект без внешнего воздействия

Для приведенного на рисунке 1.2 объекта можно синтезировать несколько систем автоматического регулирования, например: одноконтурная система регулирования, каскадная система регулирования и система с упредителем Смита.

Существует несколько методик z–преобразований в пакете Matlab. Для преобразования воспользуемся формулой пакета Matlab:

                                           (1.1)

Методы:

1.  ‘zoh’–экстраполятор нулевого порядка

2.  ‘foh’–экстраполятор первого порядка

3.  ‘imp’–импульсно независимое преобразование

4.  ‘tustin’–аппроксимация Тастина

5.  ‘prewarp’–аппроксимация Тастина с указанием критической частоты

                                   (1.2)

6.  ‘matched’–метод совпадения нулей полюсов

Если метод не указывается, программа проводит расчёт по самому простому.

Экстраполятор нулевого порядка – это устройство реализующее:

                                                  (1.3)

Экстраполятор первого порядка  – это устройство реализующее: