


























метод гармонической линеаризации и гармонического баланса позволяет определить возможность автоколебаний, их частоту, амплитуду и устойчивость.
Все реальные системы изначально являются нелинейными; поэтому, когда мы используем линейную модель реальной системы, мы прибегаем к линеаризации того или иного свойства реальной системы.
Метод гармонической линеаризации относится к приближенным методам исследования автоколебаний. Он позволяет определить условия существования и параметры автоколебаний в нелинейных системах практически любого порядка. Этот метод может быть использован также для исследования вынужденных колебательных режимов и приближенной оценки качества переходных процессов.
Метод гармонической линеаризации опирается на исследование поведения системы при гармоническом (синусоидальном) воздействии, подаваемом на вход нелинейного элемента, и замене периодической кривой на выходе нелинейного элемента первой гармоникой. Погрешность, получаемая при такой замене, сравнительно невелика, т.к. в действительности из-за последующего сглаживающего действия линейной части САУ, являющейся своего рода фильтром низкой частоты, все высокочастотные колебания не пропускаются. Практически они подавляются элементами системы, обладающими инерционностью, например, индуктивностью, механическими массами и др.
Основой метода гармонической линеаризации является предположение о том, что автоколебания приближенно можно искать в синусоидальной форме.
![]() ,
,
где а и w – искомые амплитуда и частота колебаний.
Передаточная функция нелинейного звена выглядит следующим образом:
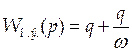
Величина q называется гармоническим коэффициентом усиления нелинейного звена.
Линеаризация заключается в замене нелинейной зависимости на прямую линию, в результате чего можно получить точную модель для случая малых отклонений от рабочей точки. Гармоническая линеаризация применяется в системах с внутренними колебаниями. Для некоторых систем вообще невозможно подобрать адекватный метод анализа и единственное, что остается сделать – это прибегнуть к имитационному моделированию. Однако учитывая специфику нелинейных систем, даже если применение какого-то метода анализа является оправданным, полученные результаты, по возможности, должны быть проверенны путем моделирования.
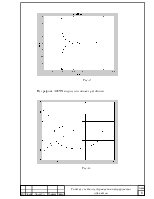
Для исследования нелинейности (релейного типа (идеальная нелинейность)) воспользуемся программой Math Cad:

Получили значения w=0.115, а=0.065, k=0.636
График изображен на чертеже (лист 22).
Далее нам необходимо промоделировать систему и убедиться, что в системе действительно присутствуют автоколебания и которые имеют значения амплитуды и частоты близкие к расчетным.
Для этого в пакете MatLab – Simulink построим нашу систему, в которой нелинейность релейного типа будет замещена операционным усилителем с коэффициентом усиления, равным 0.636.
Рассчитаем время периода колебаний:
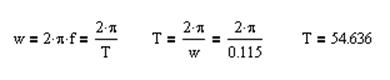
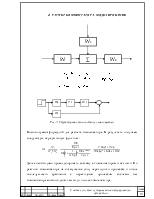
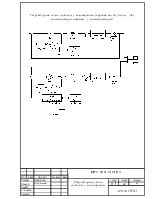
Система будет иметь вид:
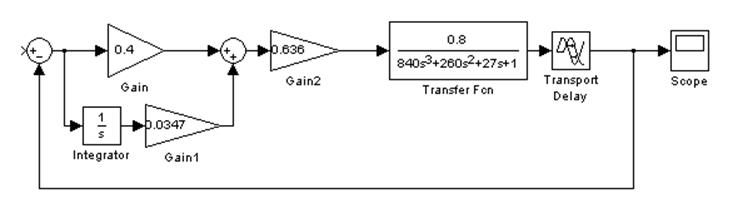
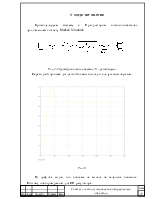
График переходного процесса
В данной курсовой работе нашей задачей было синтезировать систему управления непрерывным объектом. Курсовая работа состояла из множества важных практических задач, решая которые я в комплексе подошел к изучению синтеза систем управления.
В первом разделе курсовой работы был произведен расчет регулятора с учетом желаемого показателя колебательности Мжел.
Далее были промоделированы с помощью программы MatLab (приложение Simulink) системы с П - и ПИ – регуляторами и построены переходные процессы обеих систем. На основании переходных процессов был выбран ПИ – регулятор, т.к. П – регулятор не удовлетворяет нашим условиям.
Затем был выполнен расчет компенсатора и моделирование системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.