Санкт-Петербургский государственный политехнический университет
Институт прикладной математики и механики
Лабораторная работа №1 по дисциплине
«Численные методы в теории колебаний»
Исследование одношаговых методов численного решения задачи Коши.
Руководитель: ________ Смирнова Н. А.
Выполнили: Студенты группы 33602/2 ______Ермакова Л.Д
Ковалева Е.В.
Санкт-Петербург
2014
I.Постановка задачи
В данной
работе исследуется качество работы трех одношаговых методов численного решения
задачи Коши: явный, неявный методы Эйлера и метод средней точки. Работу этих
методов будем рассматривать в задачах о свободных и вынужденных колебаниях
линейного осциллятора. То есть будут проведены исследования методов
интегрирования ![]() - семейства, где в качестве
объекта исследований берется линейный осциллятор, поскольку его поведение уже
хорошо известно, что дает возможность грамотно проанализировать полученные
результаты. Так как существует принципиальная разница в моделировании
консервативных, слабо и сильно демпфированных систем, то при исследовании
необходимо изучить поведение численной модели для каждой из этих систем.
- семейства, где в качестве
объекта исследований берется линейный осциллятор, поскольку его поведение уже
хорошо известно, что дает возможность грамотно проанализировать полученные
результаты. Так как существует принципиальная разница в моделировании
консервативных, слабо и сильно демпфированных систем, то при исследовании
необходимо изучить поведение численной модели для каждой из этих систем.
II.Математическая модель
Движение линейного осциллятора описывается дифференциальным уравнением вида
![]() (1)
(1)
где ![]() - обобщенная координата,
- обобщенная координата, ![]() - инерционный коэффициент,
- инерционный коэффициент, ![]() - коэффициент сопротивления,
- коэффициент сопротивления, ![]() - квазиупругий коэффициент,
- квазиупругий коэффициент, ![]() - обобщенная сила. Поделив обе части
уравнения на инерционный коэффициент и введя безразмерное время
- обобщенная сила. Поделив обе части
уравнения на инерционный коэффициент и введя безразмерное время 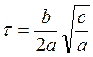 , получим:
, получим:![]() (2)
(2)
где ![]() - варьируемый параметр (имеет физический
смысл относительного затухания). Таким образом, теперь характер движения
осциллятора определяется одним параметром. В качестве начальных условий имеем:
- варьируемый параметр (имеет физический
смысл относительного затухания). Таким образом, теперь характер движения
осциллятора определяется одним параметром. В качестве начальных условий имеем:
![]() ,
, ![]() .
.
Корни
характеристического уравнения задачи (2): ![]() . В
зависимости от значений
. В
зависимости от значений ![]() получаем три различные
по своим свойствам системы:
получаем три различные
по своим свойствам системы:
1.
![]() Система без демпфирования, консервативная
система. Получаем чисто мнимые корни.
Система без демпфирования, консервативная
система. Получаем чисто мнимые корни.
2.
![]() Система с малым демпфированием. Получаем
комплексные корни с отрицательной действительной частью (несущественная
величина):
Система с малым демпфированием. Получаем
комплексные корни с отрицательной действительной частью (несущественная
величина): ![]() . Общее решение однородного уравнения
представляет собой затухающие колебания
. Общее решение однородного уравнения
представляет собой затухающие колебания ![]() .
.
3.
![]() Система с большим демпфированием. Получаем
сильно различные отрицательные действительные корни:
Система с большим демпфированием. Получаем
сильно различные отрицательные действительные корни: ![]() .
Общее решение однородного уравнения представляет собой суперпозицию убывающих
экспонент
.
Общее решение однородного уравнения представляет собой суперпозицию убывающих
экспонент ![]() .
.
Вводя
векторную переменную 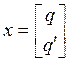 , получим нормальную форму задачи
Коши:
, получим нормальную форму задачи
Коши:
![]() (3) где
(3) где 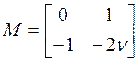 ,
, 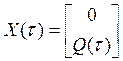 .
Тогда начальные условия будут иметь вид:
.
Тогда начальные условия будут иметь вид: ![]() .
.
III.Описание методов
Имеется задача Коши:
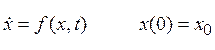 (4)
Требуется решить её численными методами интегрирования.
(4)
Требуется решить её численными методами интегрирования.
Рассматривается однопараметрическое семейство методов Рунге-Кутты:
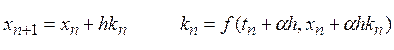 . В зависимости от значений параметра
. В зависимости от значений параметра ![]() получаем:
получаем:
1.
![]() Явная схема метода Эйлера:
Явная схема метода Эйлера: ![]() . Имеет первый порядок точности.
. Имеет первый порядок точности.
2.
![]() Неявная схема метода Эйлера:
Неявная схема метода Эйлера: ![]() . Имеет первый порядок точности.
. Имеет первый порядок точности.
3.
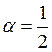 Метод средней точки:
Метод средней точки: 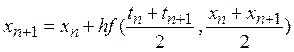 . Имеет второй порядок точности.
. Имеет второй порядок точности.
Устойчивость методов.
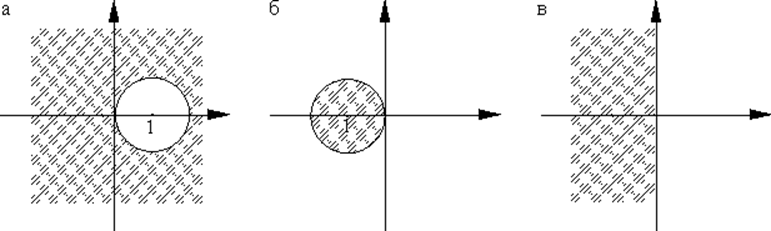
Области устойчивости
а) неявного метода Эйлера; б) явного; в) метода средней точки
IV.Свободное движение
1.Система
без демпфирования (![]() ,
,![]() )
)
Консервативная
система. Получаем чисто мнимые корни. Для данной системы за шаг интегрирования
принимается значение ![]() .
.
Так как демпфирование сказывается, прежде всего, на скорости потерь энергии, то целесообразно в случае консервативной системы получить либо зависимость энергии от времени, либо амплитуды колебаний от времени, что, в данном случае, одно и то же, так как энергия пропорциональна квадрату амплитуды колебаний.
![]() Явная схема метода Эйлера
Явная схема метода Эйлера
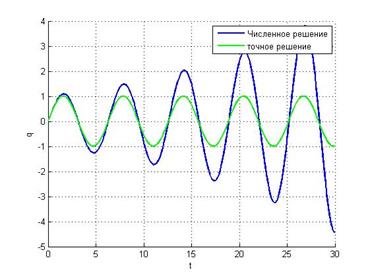
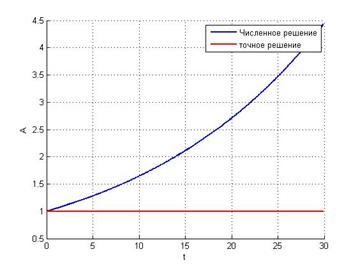
Видим,
что в данном методе амплитуда со временем будет расти, что не соответствует
консервативной системе. Значит, метод не применим. В этом также можно
убедиться, если заметить,
что при чисто мнимом
собственном значении ![]() алгоритм
неустойчив при любом шаге интегрирования.
алгоритм
неустойчив при любом шаге интегрирования.
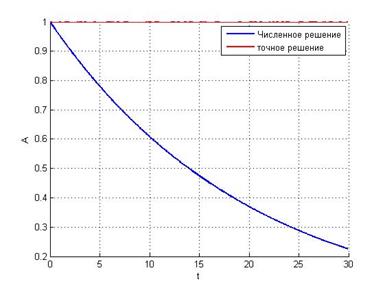
![]() Неявная схема метода Эйлера
Неявная схема метода Эйлера
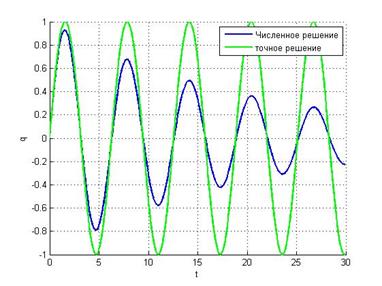
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.