Исследование трех одношаговых методов численного решения задачи Коши: явный, неявный методы Эйлера и метод средней точки, страница 2

Неявная схема Эйлера  воспроизводит колебания с убывающей амплитудой, что также не соответствует консервативной системе. Это естественное следствие того, что мнимая ось целиком лежит внутри области устойчивости метода. Значит, и этот метод не применим.

  Метод средней точки

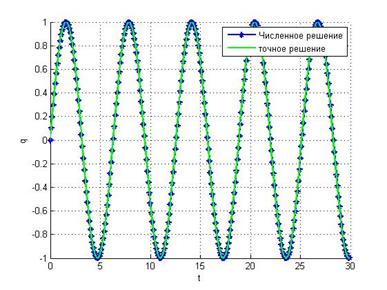
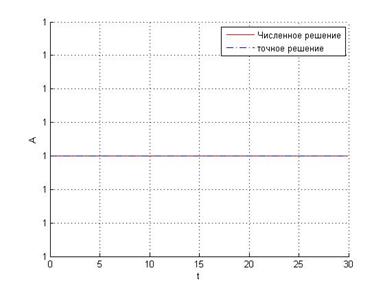
Видим, что метод средней точки воспроизводит колебания с постоянной амплитудой. Это определяется тем, что здесь мнимая ось является границей области устойчивости как точного, так и численного решений.

Таким образом, для решения задач о колебаниях консервативных механических систем целесообразно использовать метод средней точки. Он сохраняет энергию линейной консервативной механической системы.

2.Система с малым демпфированием()

Общее решение однородного уравнения – затухающие колебания: . Корни характеристического уравнения:  .

  Явный метод Эйлера

h = 0.1: Из нижеприведенных графиков видно, что при таком шаге интегрирования корни  лежат вне области устойчивости данного метода.

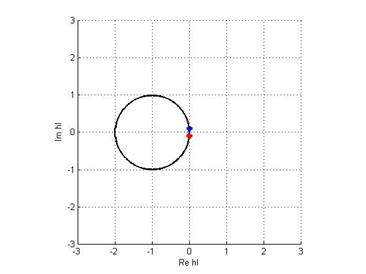
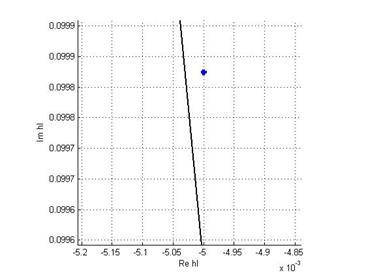
Убедиться в этом можно, взглянув на график зависимости обобщённой координаты от времени:

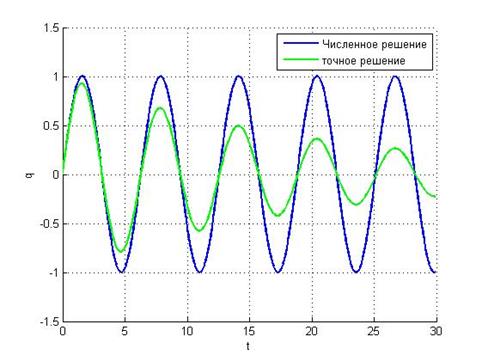
h = 0.5:  Наблюдаемтакую же картину. При данном шаге метод неустойчив.

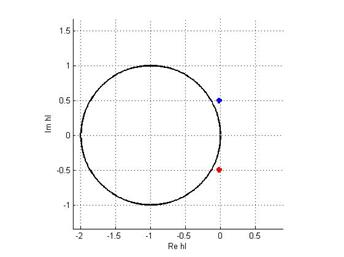
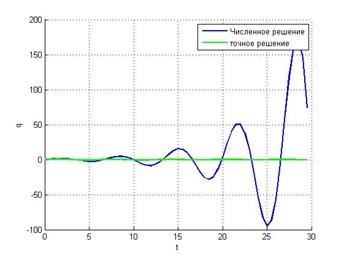
h = 0.01: А вот уже при таком выборе шага корни попадают в единичную окружность, что дает устойчивость метода.

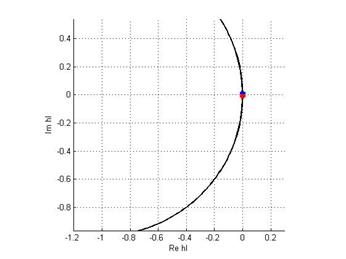
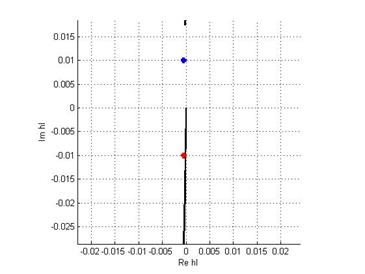
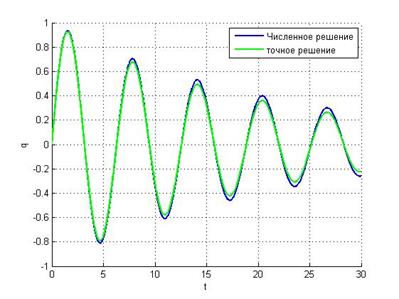Значит,  для системы с малым демпфированием явный метод Эйлера применим при очень маленьком шаге. При увеличении будем получать неустойчивость.

  Неявный метод и метод средней точки

Эти методы моделирует слабо-демпфированную систему только как слабо-демпфированную. Сравним их при разных величинах шага.

h=0.01

Неявный метод Эйлера                                              Метод средней точки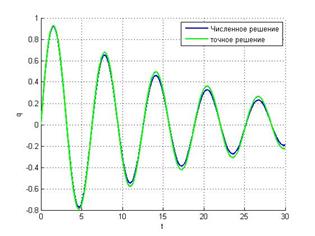                    

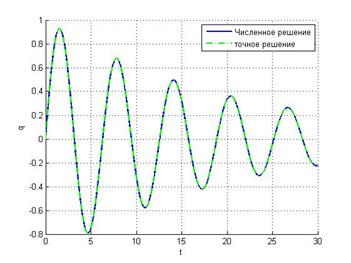
h = 0.1

Неявный метод Эйлера                                                   Метод средней точки

 

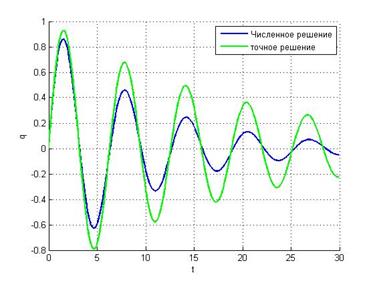
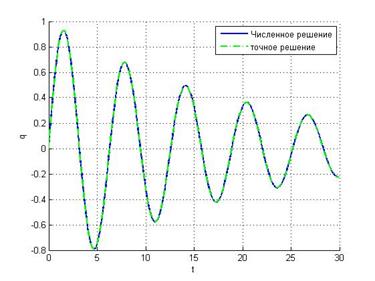
h = 0.5

Неявный метод Эйлера                                               Метод средней точки

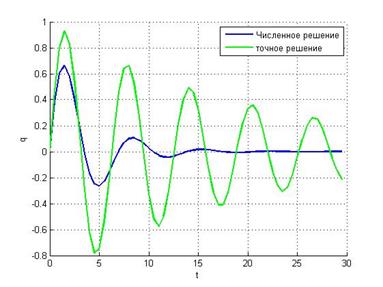
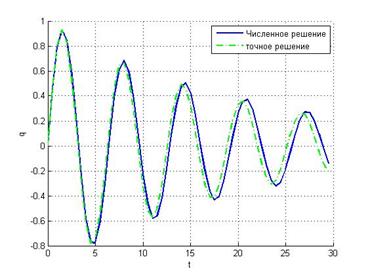
Видим, что метод средней точки при увеличении шага работает лучше, чем неявный метод Эйлера.

3.Система с большим демпфированием ()

Получаем действительные отрицательные корни характеристического уравнения: , . В данном случае решение состоит из двух затухающих экспонент: .  Колебательность наблюдаться не будет. Для такой системы стоит увеличить шаг интегрирования и посмотреть, как это влияет на работу каждого из методов.

  Явная схема метода Эйлера

h = 0.1                                                                             h=0.4

                 

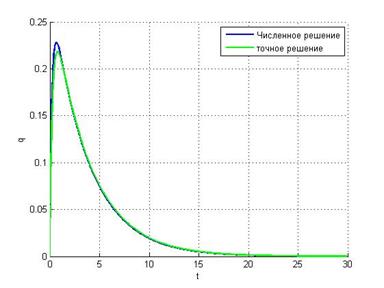
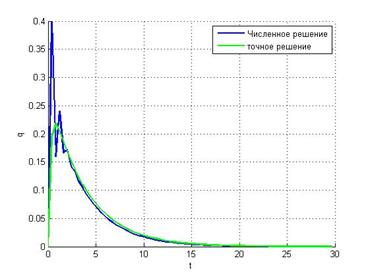
h =1

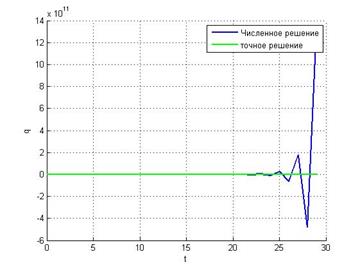
Из вышеприведенных графиков видно, что при малых значениях  явный метод дает вполне хорошее приближение к точному решению. Однако при   явная схема метода Эйлера дает отрицательное значение переходному множителю  () , что индуцирует неоправданную колебательность при воспроизведении монотонно убывающей экспоненты, а при 2 имеем , что свидетельствует о неустойчивости метода.

  Неявная схема метода Эйлера

h = 0.1                                                                        h = 0.5

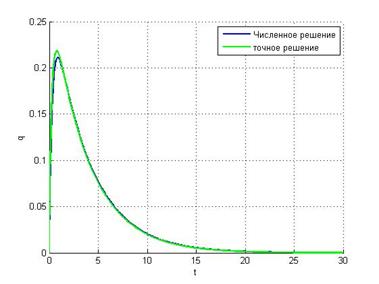
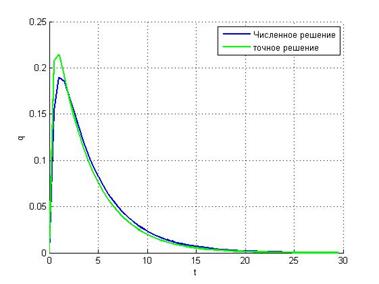
h = 1

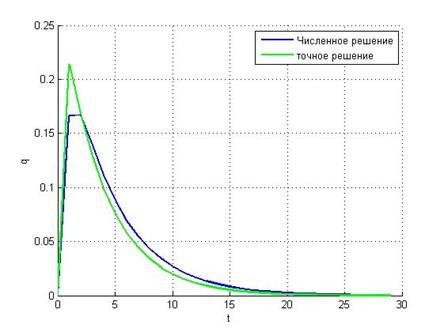
Видим, что неявная схема метода Эйлера даёт адекватное воспроизведение убывающей экспоненты даже при большом шаге интегрирования. Здесь имеем, что при   переходный множитель   , как и в точном решении.

  Метод средней точки

h=0.1

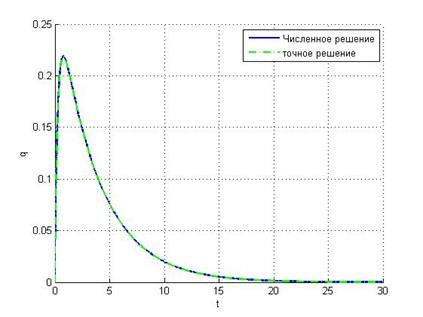
h=0.5                                                                                                       h=1

 

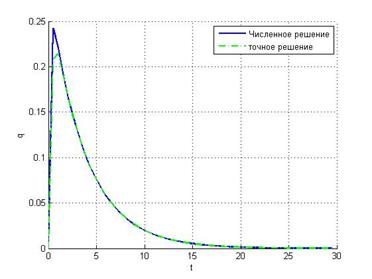
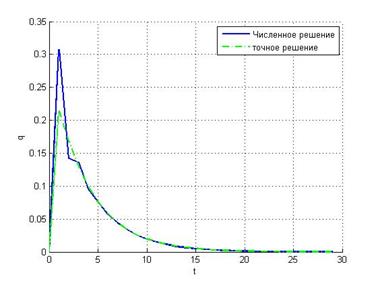
Метод средней точки даёт наилучшее приближение к точному решению при малых шагах интегрирования, однако при 2 величина 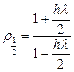 становится отрицательной.

Значит, данный метод при большом шаге интегрирования воспроизводит быстро убывающую экспоненту в виде знакочередующейся, очень медленно убывающей по модулю последовательности точек.

IV.Вынужденное движение

В данной части работы необходимо исследовать качество работы указанных выше трех алгоритмов в задаче о вынужденных колебаниях осциллятора с малым демпфированием при действии на него гармонической вынуждающей силы.  Движение линейного осциллятора под действием такой силы описывается дифференциальным уравнением вида

                                                                                       (5)

Коэффициент относительного затухания:  .

Особенности этой работы заключаются в том, что устойчивость рассматриваемой системы не зависит от правой части уравнения (5), а устойчивость различных методов для систем с малым демпфированием была рассмотрена выше. Нам необходимо рассмотреть, что происходит с системой в области резонанса,  снимая амплитудно-частотную характеристику (АЧХ) в зоне частот, близких к резонансу.