Исследование трех одношаговых методов численного решения задачи Коши: явный, неявный методы Эйлера и метод средней точки, страница 3

Обозначим за = и применим преобразование Лапласа к правой и левой частям уравнения (5). Получим: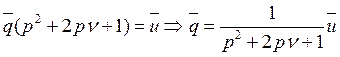  

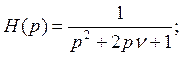
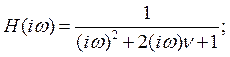
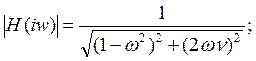
При моделировании вынужденных колебаний возникает проблема выделения частного решения. И координата и скорость будут содержать два колебательных процесса: сопутствующие колебания и вынужденные колебания.

Сопутствующие колебания являются затухающими, вопрос в том, через какое время они затухнут. Из теории автоматического управления мы знаем, что процесс затухания можно считать закончившимся через время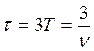. Для большей надежности возьмем время.

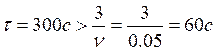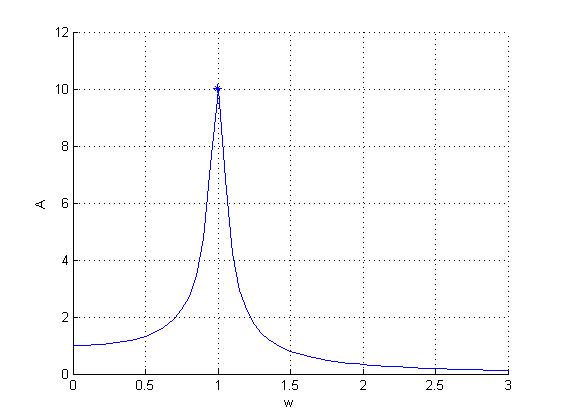
В нашем случае ;

  Явный метод Эйлера

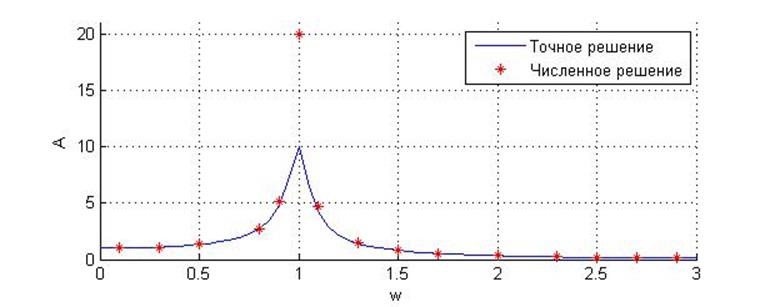
Видим, что явный метод даёт хороший результат на высоких и низких частотах. Но вблизи резонансной частоты амплитуды сильно рознятся.

  Неявный метод Эйлера

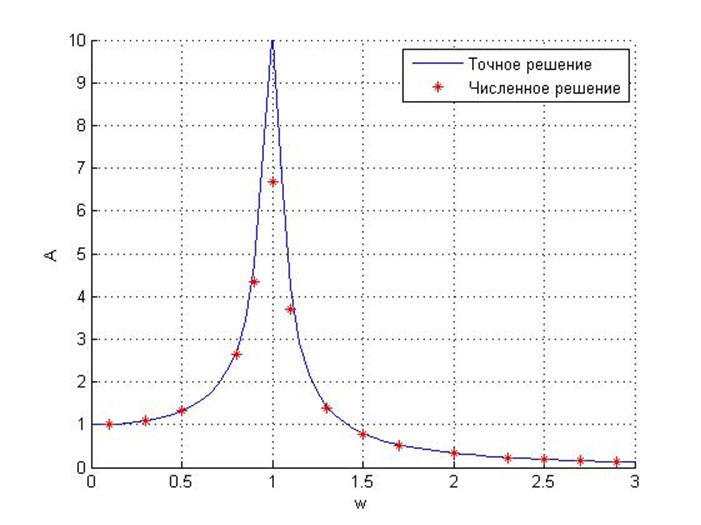
Неявный метод, как и явный, допустимо использовать только для низких и высоких частот, избегая области резонанса.

  Метод средней точки

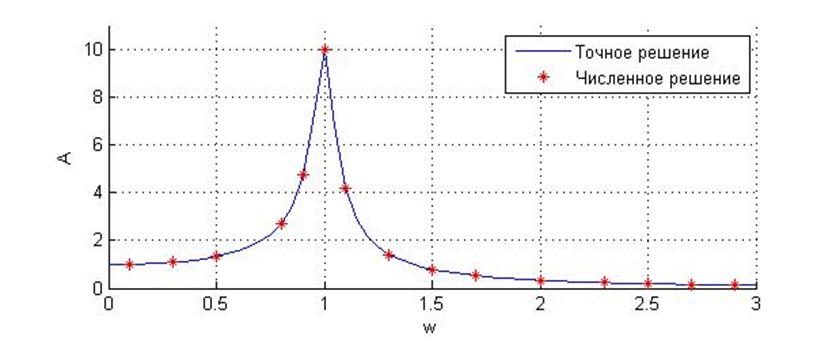
Графики точного решения и приближенного практически совпадают. Это говорит о том, что мы можем спокойно использовать метод средней точки для гармонического осциллятора при малом демпфировании на всем диапазоне частот.

III.Выводы

Таким образом, можно сделать следующие выводы:

1) Для консервативных систем получаем, что в явном методе амплитуда со временем будет расти, что не соответствует консервативной системе. Значит, метод не применим. В этом также можно убедиться, если заметить, что при чисто мнимом собственном значении  алгоритм неустойчив при любом шаге интегрирования.

Неявная схема Эйлера  воспроизводит колебания с убывающей амплитудой, что также не соответствует консервативной системе. Это естественное следствие того, что мнимая ось целиком лежит внутри области устойчивости метода. Значит, и этот метод не применим.

Метод средней точки воспроизводит колебания с постоянной амплитудой. Это определяется тем, что здесь мнимая ось является границей области устойчивости как точного, так и численного решений.

Таким образом, для решения задач о колебаниях консервативных механических систем целесообразно использовать метод средней точки. Он сохраняет энергию линейной консервативной механической системы.

2) Для систем с малым демпфированием получаем, что для явного метода Эйлера важно выбирать шаг интегрирования таким, чтобы корни  лежат в области устойчивости данного метода. В большинстве случаев это составляет сложную задачу, поэтому данный метод не рекомендован для моделирования процесса в слабо демпфированной системе.

Методы средней точки и неявный метод Эйлера моделирует слабо-демпфированную систему только как слабо-демпфированную. Сравнивая их при различном шаге, приходим к выводу, что метод средней точки при увеличении шага показывает лучшие результаты, поэтому именно этот метод и рекомендуем использовать.

3) Для систем с большим демпфированием получаем, что для явного метода Эйлера получаем различные результаты в зависимости от величины . При   явная схема метода Эйлера дает отрицательное значение переходному множителю  () , что индуцирует неоправданную колебательность при воспроизведении монотонно убывающей экспоненты, а при 2 имеем , что свидетельствует о неустойчивости метода. Поэтому нужно подбирать эту величину такой, чтобы избежать колебательность и неустойчивость. А для жестких систем явный метод требует нереально маленький шаг.

Для неявной схемы метода Эйлера мы получаем адекватное воспроизведение убывающей экспоненты даже при увеличении шага интегрирования. Здесь имеем, что при   переходный множитель   , как и в точном решении.

Метод средней точки даёт наилучшее приближение к точному решению, однако при 2 величина 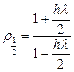 становится отрицательной.

Значит, данный метод при увеличении шага интегрирования воспроизводит быстро убывающую экспоненту в виде знакочередующейся, очень медленно убывающей по модулю последовательности точек.

Таким образом, для исследования жестких систем рекомендуем неявный метод Эйлера.

4)Для вынужденных колебаний получаем, что явный и неявный методы Эйлера не применимы в области резонанса. Для остальных областей методы дают хорошие результаты.

Метод средней точки лучше всего подходит для  исследования данной системы, однако важно понимать, что это чревато большей затратой времени.