Дифференциальные уравнения. Линейное дифференциальное уравнение первого и второго порядка. Дифференциальные уравнения в полных дифференциалах

Тема 4. Дифференциальные уравнения

Лекция 4

Основные сведения

Уравнение, содержащее производные или дифференциалы неизвестной функции:

 ¨ одного переменного, называют обыкновенным дифференциальным  уравнением;

¨ две или больше переменных, называется дифференциальным уравнением в частных производных.

Наибольший порядок производной или дифференциала, входящих в уравнение, называют порядком уравнения.

Пример 1. 

x²y¢ + 5xy = y² – обыкновенное диффренциальное уравнение первого порядка,

F(x , y , y¢) = 0 – общий вид дифференциального уравнения первого порядка.

y¢¢ - 4xyy¢ = x² - обыкновенное диффренциальное уравнение второго порядка,

F(x , y , y¢, y¢¢) = 0 – общий вид дифференциального уравнения второго порядка,

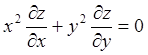- уравнение в частных производных первого порядка,

F(x , y , ¶z/¶x, ¶z/¶y) = 0 – общий вид дифференциального уравнения в частных производных первого порядка.

Решением уравнения n-го порядка называют всякую функцию, имеющую на рассматриваемом промежутке производную порядка п и обращающую уравнение в тождество.

Обыкновенные дифференциальные уравнения

Дифференциальные уравнения первого порядка

Общий вид уравнения первого порядка F(x, y, y') = 0 или y¢= f(x, y).

Простейшим уравнением первого порядка является уравнение у' = j(x), общее решение

 которого задается в виде
Решение y = f(x,C), где С - произвольная постоянная, называют общим решением уравнения первого порядка и задает бесконечное семейство решений.

При фиксировании С получают частное решение.

Построенный на плоскости x0y график всякого решения дифференциального уравнения называется интегральной кривой этого уравнения.

Решение уравнения первого порядка в виде Ф(х,у,С) = 0, называют общим интегралом.

Задача Коши ставится следующим образом: найти решение уравнения , удовлетворяющее начальным условиям у(х₀) =y₀ , где х₀ и y₀   - заданные числа.

Теорема Коши

            Если функция f(x,y) непрерывна и имеет непрерывную производную , то решение дифференциального уравнения y¢= f(x, y) при начальном условии y(x₀) = y₀  существует и единственно.

Это означает, что надо найти решение уравнения, удовлетворяющее начальным условиям y(x₀) = y_0;  через точку (x₀,y₀) проходит единственная интегральная кривая данного уравнения.

Пример 2. Найти решение (задачи Коши) уравнения   у' = sin х,  при условии  у₀(p/2) = 1 .

Решение.   y¢ =,    = sinx,  dy=sinxdx,   òdу = òsin xdx,    y = - cos х + С .

При этом  y₀(p/2) =1 имеем  1= - cos  + С = 0 + C, откуда  С = 1.

Таким образом, частным решением уравнения у' = sin х является  у = 1- cosx.

1. Дифференциальное уравнение с отделенными переменными

Это уравнение имеет вид:     f(x) + g(y)×y¢=0

Алгоритм решения

Заменяя  y¢ на  и умножая на dx,  получаем   f(x)dx+g(y)dy=0.

Теперь для решения уравнения достаточно проинтегрировать полученное уравнение:

                                   ò f(x)dx + ò g(y)dy = С

Находя интегралы, получим:    ò f(x)dx = F(x),  ò g(y)dy = G(y) или

F(x) + G(y) = С , называемое общим интегралом.

Если решить это уравнение относительно y, то получается равенство y = j(x) + C, правая часть которого есть общее решение дифференциального уравнения.

Пример 3.

Решить уравнение 2x +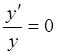 

Заменяя  y¢ на  и умножая на dx,  получаем: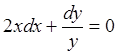

Интегрируя 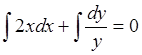, находим: откуда  и .

Так как е^С =const, то заменив е^С через С₁, а затем снова записав С вместо С₁, запишем

 общее решение:      .

Пример 4.

Решить уравнение 2xdx + (5y⁴ + cosy)dy=0

Находим общий интеграл: x²+ y⁵+ siny = C

Хотя выразить отсюда y через x и C мы не умеем, но все же считаем уравнение решенным.

2. Дифференциальное уравнение с отделяющимися переменными

Это уравнение имеет вид: f₁(x)×g₂(y) + f₂(x)×g₁(y)×y¢ = 0

Алгоритм решения

Заменяя  y¢ на  и умножая на dx,  преобразуем уравнение к виду: f₁(x)×g₂(y)dx + f₂(x)×g₁(y)dy = 0

Теперь разделив последнее уравнение на произведение f₂(x)×g₂(y), приходим к уравнению:

                                              

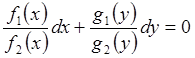
в котором переменные уже отделены.

Теперь для решения уравнения достаточно проинтегрировать полученное уравнение:

                                              

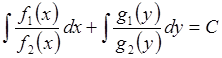
и получитьF(x) + G(y) = С , называемое общим интегралом.

Однако встречаются дифференциальные уравнения, решением которых могут быть также постоянные функции у = а или х = b , если х = b или у = а являются корнями уравнения f₂(x)×g₂(y) = 0 . Эти решения могут не содержаться в интегральном уравнении ни при каких значения произвольной постоян­ной С. Тогда их называют особыми решениями. Так, например, функция y=(x+C)² является общим решением дифференциального уравнения y¢ ²=4y. Однако это уравнение имеет еще особое решение y=0, которое не получается из общего решения ни при каком значении постоянной С.

Пример 5.

Решить уравнение 2xsinydx + (x² + 3)cosydy = 0

Разделив на (x² + 3) siny, получаем: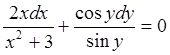

Интегрируя, находим , , ,

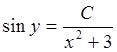 и окончательно общее решение .

3. Линейное дифференциальное уравнение первого порядка

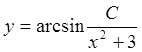Линейным дифференциальным уравнением первого порядка называется такое дифференциальное уравнение, в которое неизвестные элементы y иy¢ входят в первых степенях, не перемножаясь между собой.

Уравнение имеет вид: A(x)y¢ + B(x)y + C(x) = 0

Разделив уравнение на A(x) и полагая 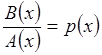,  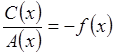, придадим вид:

y¢ +p(x)y=q(x)

Алгоритм решения

Он основан на простом замечании, что любую величину h (переменную или постоянную) можно представить в форме произведения двух сомножителей h = u× v, причем один из них(например, v)  можно выбирать по своему желанию (кроме v=0).

            Если искать его решение в виде у = и(х)• v(x), то получаем

u'v + uv' + p(x)uv = q(x)

      vu' + (v' + p(x)v)u = q(x).

Выберем v(x) так, чтобы  v¢ + p(x)v=0, тогда v(x)u¢ = q(x),

Решая v¢ + p(x)v=0, 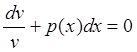 , отсюда  и беря С=0 и понимая под  какую-нибудь одну первообразную для , найдем сначала , а затем и саму функцию u. В результате получится v(х)=A(x), где A(x) какая-то (известная!) функция.

Тогда u¢A(x) = q(x) и, значит, 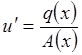, а u(х)=B(x)+C),  откуда получаем:

                                               y=[B(x)+C)]×A(x)

Пример 6. Найти решение задачи Коши y¢ - y = e^-х   при условииy(0)=2, (т.е. y=2 при x=0)

y =uv,  u¢v + v¢u – uv = e^-х, ,  u¢v + (v¢ – v)u = e^-х,

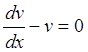1. Положим v¢ – v=0, тогда  или 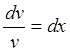 и далее 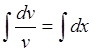, lnv = x и v = e^x
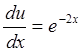2. u¢ v = e^-х , u¢ e^x =e^-x, , du =e^-2xdx, òdu =òe^-2xdx, u=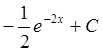

Общее решение  y=uv=(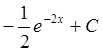)e^x=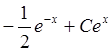

 Подставляя y(0)=2, имеем -1/2+C=2, C=5/2 и решение задачи Коши имеет вид: y=.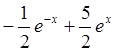

Линейное уравнение второго порядка с постоянными коэффициентами

Уравнение имеет вид  у¢¢ + ру¢ + qy = f(x) , где р и q - постоянные коэффициенты.

Если f(x) - нулевая функция, то уравнение называют однородным.

Задача Коши  позволяет выделить одно конкретное частное решение. Задача ставится так:  найти решение у(х) уравнения , удовлетворяющее начальным условиям у(х₀) = y₀, y'(x₀) = y₁, где х₀, у₀, у₁ - заданные числа.

Однородное уравнение