Комплексные числа. Операции над комплексными числами

Лекция 6

Комплексные числа

1. Основные сведения

2. Операции над комплексными числами

3. Формула Муавра

4. Формула Эйлера

Основные сведения

Множество действительных чисел есть подмножество множества комплексных чисел.,т.е. R Ì C.

Алгебраическая форма комплексного числа записывается  в виде z= x+ yi, где:

 x = Re z - действительная часть, y = Im z - мнимая часть z, (x,y)Î R; i - мнимая единица, i² = -1.

            Геометрически каждое комплексное число z =х+ iу изображается точкой М (х; у) координатной плоскос­ти х0у. В этом случае плоскость х0у на­зывают комплексной числовой плоскостью, или плос­костью комплексного переменного z.

Тригонометрическая форма комплексного числа записывается  в виде z = x+ yi =

 = r×(cosj + i×sinj), где в полярных координатах:  модуль zесть r = |z| =  и

аргумент z есть j = arg z  точки М, являю­щейся изображением комплексного числа z = x+ iy.

Аргумент z  может быть определен из равенств cosj = или  sinj =.

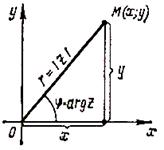
Аргумент z определяется с точностью до 2kp,   kÎ Z. 

Главным значением аргумента будем считать значение аргумента argz из промежутка [0,2p[. 

Общее значение  аргумента  Arg z = arg z  + 2pk,   k Î Z.

Операции сложения и умножения комплексных чисел выполняют так же,  как аналогичные операции с много­членами с учетом того, что i² = -1.

Число называют сопряженным числу z = x + yi.

Отметим, что z - действительное число. Это используют при выполнении операции деления комплексных чисел.

Пример 1. Вычислить  (2+i)×(1-i)= 2×1 + i×1 - 2×i - i² = 2 + i - 2i +1 = 3 - i.

Пример 2.  Вычислить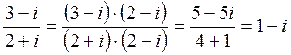

Операции над комплексными числами

Если даны два комплексных числа z = r×(cosj + i×sinj)  и  z₁ = r₁×(cosj₁ + i×sinj₁) то:

1⁰.   z ± z₁=(x ± x₁)+ i(y ± y₁)  

1⁰.    z× z₁= (xx₁ –yy₁) + i(xy₁+x₁y) = r×r₁×[cos(j+j₁)+i×sin(j+j₁)];

2⁰. 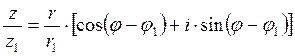  , если z₁¹ 0;

3⁰.     -  формула Муавра,  nÎ N

Корень степени n  из комплексного числа z имеет п различных значений, которые можно вычислить по формуле:

4⁰. 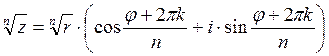, k =0,1,2,…,n-1.

5⁰. lnz = ln r + (j + 2kp)i,  kÎZ.

Пример 3. Вычислить (1- i)¹⁵.

            z = 1- i; x =1, y = -1, тогда: |z|=,  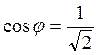,  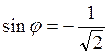 Þ (II -аячетверть)  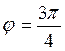Þ применим 3⁰, тогда по формуле Муавра:z¹⁵ = (1 - i)¹⁵ =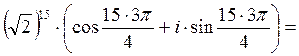

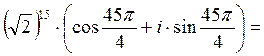
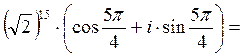
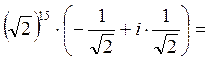=2⁷(-1+ i).

Формула Эйлера