Пусть дана функция f(z), аналитическая в некоторой окрестности точки а.
Тогда в круге сходимости эта функция может быть представлена рядом Тейлора:
f(z)=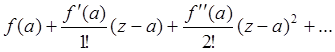
а само равенство называют разложением функции в ряд Тейлора.
Замечание: многоточие, которым заканчивается правая часть функции f(z), символизирует тот факт, что точное равенство достигается за счет бесконечного множества слагаемых. Поэтому последнего слагаемого нет.
Пример 1.
Разложить в ряд Тейлора по степеням бинома (z – i) функцию f(z) = z5, а = i.
Решение:
Находим производные функции f(z) = z5: ![]() .
.
Определим значения производных в
точке a = i: ![]() .
.
Отсюда ![]() -
многочлен 5-ой степени.
-
многочлен 5-ой степени.
Если функция f(z) имеет в точке а производные до порядка n включительно, то ее можно представить формулой Тейлора порядка n:
f(z) =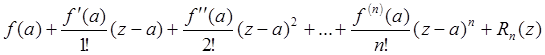 ;
; 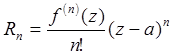 .
.
Положив а = 0, можно разложить функцию f(z) в ряд Маклорена: f(z)=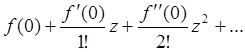
|
Разложим ez и eiz в ряд Маклорена:
для ez для eiz |
|
Применив разложение в ряд к функциям sinz и cosz, получим:
|
|
|
f(z)=ez f(0)=1 f¢(z)=ez f¢(0)=1 f¢¢(z)=ez f¢¢(0)=1 f¢¢¢(z)=ez f¢¢¢(0)=1 ……… ……… f(n)(z)=ez f(n)(0) =1 ………. ……. |
f(z)=ezi f(0)=1 f¢(z)=iezi f¢(0)=i f¢¢(z)=-ezi f¢¢(0)=-1 f¢¢¢(z)=-iezi f¢¢¢(0)=-i ……… ……… f(n)(z)=inezi f(n)(0) =1 ………. ……. |
||
Произведя замену z на iz для функции ez и разделив eiz на Reeiz и Imeiz части, легко увидеть, что ezi есть сумма cosz и i× sinz.
Cоотношения между функциями, выражаемые как:
![]()
![]() ;
; 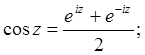
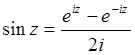 ;
;
называются формулами Эйлера.
Рассмотрим два ряда:
1. 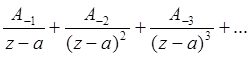 ,
область сходимости которого определяется неравенством r <| z-a|
и
,
область сходимости которого определяется неравенством r <| z-a|
и
2. ![]() ,
область сходимости которого определяется неравенством | z-a| < R.
,
область сходимости которого определяется неравенством | z-a| < R.
При условии r < R, областью сходимости ряда,
полученного сложением вышеперечисленных рядов, 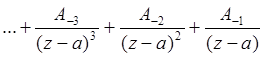 +
+![]()
|
рис.1
|
служит кольца r < | z-a|< R, ограниченное концентрическими окружностями с центром в точке a и радиусами z и R (рис. 1).
Пример 2.
Исследовать сходимость ряда 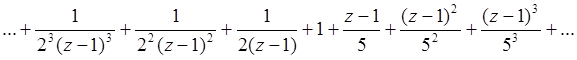 .
.
Решение:
Рассмотрим два ряда:
1 – ый ряд 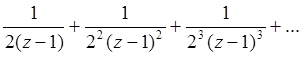
Чтобы представить 1–ый ряд в виде степенного ряда 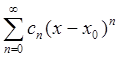 , надо в нем положить (z – 1) =
, надо в нем положить (z – 1) =![]() . Тогда
получим степенной ряд
. Тогда
получим степенной ряд 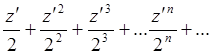 , радиус сходимости которого найдем,
применив формулу Даламбера r =
, радиус сходимости которого найдем,
применив формулу Даламбера r =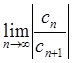 :
: 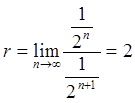 .
.
Следовательно ряд сходится , если
|![]() |<
2, т.е.
|<
2, т.е. 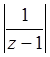 <
2 Þ |z - 1| >
<
2 Þ |z - 1| >![]() .
.
1-ый ряд сходится вне круга радиуса r = 1/2 с центром в точке z = 1.
2 – ой ряд 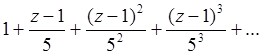
По формуле Даламбера радиус сходимости R =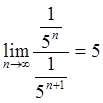 и ряд сходится
, если |
и ряд сходится
, если |![]() |<
5.
|<
5.
2-ой ряд сходится в круге радиуса R = 5 с центром в точке z = 1.
Ответ: областью сходимость исходного ряда является кольцо 1/2< | z -1 |< 5.
Если f(z) - однозначная и аналитическая функция в кольце г < | г - а |< R, то эта функция в указанном кольце может быть представлена в виде суммы ряда Лорана:
f(z) = 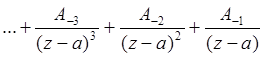 +
+
![]()
Ряд 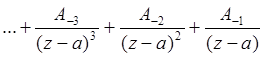 - главная часть ряда Лорана, а
- главная часть ряда Лорана, а
ряд ![]() - правильная
часть ряда Лорана.
- правильная
часть ряда Лорана.
Коэффициенты
этого ряда можно вычислить по формуле 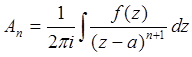 ,
nÎ Z. Коэффициент А-1
называется вычетом функции f(z)
относительно изолированной особой
,
nÎ Z. Коэффициент А-1
называется вычетом функции f(z)
относительно изолированной особой
точки z = a.
Если ряд Лорана содержит главную часть, то а называется изолированной особой точкой.
Особая точка z = a называется устранимой, если существует конечный
предел ![]() . Особая точкаявляется устранимой, если главная часть разложения в ряд Лорана
отсутствует.
. Особая точкаявляется устранимой, если главная часть разложения в ряд Лорана
отсутствует.
Пример3.
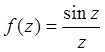 в точке z = 0
является устранимой особой точкой, так как
в точке z = 0
является устранимой особой точкой, так как 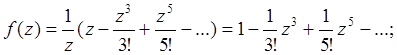
Особая точка z = a
называется существенно особой,
если ![]() не существует.
не существует.
Пример 4.
![]() в
точке z=0 имеет существенно особую точку,
так как
в
точке z=0 имеет существенно особую точку,
так как 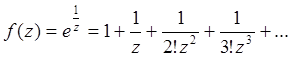 .
.
Особая точка z = a
называется полюсом функции f(z),
если ![]() .
.
Пример 5.
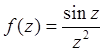 в
точке z =0 является
полюсом первого порядка, так как
в
точке z =0 является
полюсом первого порядка, так как 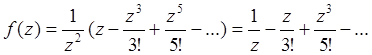 .
.
Практикум 4
1. Разложить sinx по степеням (x-p/4).
Решение: f(x)= sinx = sinp/4+(1/1!)×cosp/4×(x-p/4)-(1/2!)× sinp/4×(x-p/4)2-(1/3!)×cosp/4×(x-p/4)3+…=
=![]() [1+(1/1!)×(x-p/4)-(1/2!)×(x-p/4)2-(1/3!)×(x-p/4)3+…].
[1+(1/1!)×(x-p/4)-(1/2!)×(x-p/4)2-(1/3!)×(x-p/4)3+…].
2. Найти область сходимости ряда 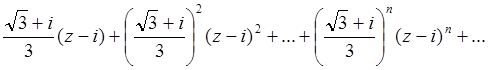
Решение: R=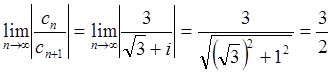 .
.
Областью сходимости ряда является круг |z
– i|< ![]() .
.
3. Исследовать сходимость ряда Лорана 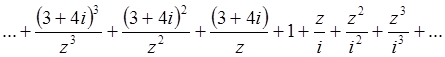
Решение: Рассмотрим два ряда: оба ряда являются
геометрическими прогрессиями со знаменателями соответсвенно 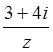 и
и ![]() .
Они сходятся , если
.
Они сходятся , если 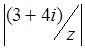 < 1 и
< 1 и ![]() <1 соответственно.
<1 соответственно.
Так как ![]() = 5, то |5/z|< 1 Þ |z| >5, и
= 5, то |5/z|< 1 Þ |z| >5, и ![]() =
1 Þ|z| < 1, полученные неравенства несовместны и
данный ряд не сходится ни в одной точке плоскости.
=
1 Þ|z| < 1, полученные неравенства несовместны и
данный ряд не сходится ни в одной точке плоскости.
4.Разложить в ряд Лорана по степеням z функцию f(z)=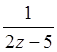 в
окрестности точки z =0.
в
окрестности точки z =0.
Решение: Представим функцию в виде: 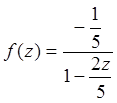 .
.
Дробь 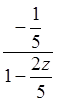 можно
рассматривать как сумму бесконечно убывающей геометрической прогрессии
можно
рассматривать как сумму бесконечно убывающей геометрической прогрессии 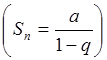 с первым членом а = -1/5 и
знаменателем q=
с первым членом а = -1/5 и
знаменателем q= ![]() <1.
(Из
<1.
(Из 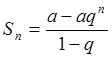 при |q|< 1, qn ®
0)
при |q|< 1, qn ®
0)
Тогда в окрестности точки z =0 выполняется неравенство |q|=![]() <
1 и областью сходимости ряда является круг
<
1 и областью сходимости ряда является круг ![]() <
<![]() .
.
А ряд будет иметь вид: 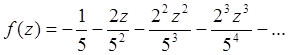 ,
или
,
или 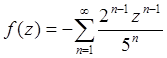 .
.
Особая точка z = 0 является устранимой, так как видно, что это разложение содержит только правильную часть ряда Лорана.
5.Разложить в ряд Лорана функцию 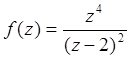 по степеням z
– 2.
по степеням z
– 2.
Решение: Пуcть z - 2 = t, тогда f(z) = 16/t2 + 32/t +24 +8t +t2 = 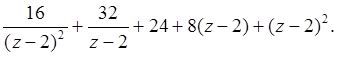
Главная часть содержит два члена, а правильная – три.
Так как разложение содержит конечное число членов, то оно справедливо для любой точки плоскости, кроме z =2.
Точка z =2 является полюсом второго порядка.
Вычетом этой функции относительно полюса z =2 является коэффициент А-1 при (z – 2)-1, т.е. 32.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.