Занятие 6. Решения СЛУ.Учебные вопросы: 1. Формулы Крамера 2. Решение системы методом обратной матрицы 3. Метод Гаусса |
4. Формулы Крамера (для системы, в которой число уравнений равно числу неизвестных)
Система линейных уравнений, в которой число уравнений равно числу неизвестных
(m=n) и определитель матрицы системы не равен 0 (D¹0), имеет единственное решение, которое определяется по формулам Крамера:
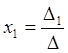
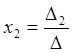 …..
…..
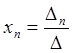
где D — определитель матрицы системы;
Dn — определитель, получаемый из определителя D заменой n - го столбца столбцом свободных членов.
Пример 2. Решить систему уравнений
![]()
![]()
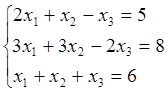 D
=
D
= ![]()
![]()
![]() =
= ![]()
![]()
![]() =
(-1)3+3×
=
(-1)3+3×![]()
![]() =15
– 10 = 5¹0
=15
– 10 = 5¹0
Система имеет единственной решение, которое можно найти по формулам Крамера:
![]()
![]()
![]() D1=
D1=![]()
![]()
![]() =
= ![]()
![]()
![]() =
(-1)3+3×
=
(-1)3+3×![]()
![]() =
55 – 40 =15
=
55 – 40 =15
![]()
![]() D2=
D2=![]()
![]()
![]() =
=
![]()
![]()
![]() = (-1)3+3×
= (-1)3+3×![]()
![]() = 60 – 55 = 5
= 60 – 55 = 5
![]()
![]() D3 =
D3 = ![]()
![]()
![]() =
=![]()
![]()
![]() = (-1)3+3×
= (-1)3+3×![]()
![]() = 10
= 10
По формуле
Крамера находим: х1=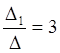 , х2 =
, х2 =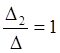 , х3=
, х3=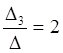 .
.
5. Решение системы методом обратной матрицы
1) Найти обратную матрицу матрицы А=![]()
![]()
Составим систему AX=Y,
те-есть систему 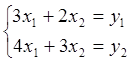 Þ
Þ
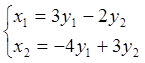 следовательно
следовательно
А-1=![]()
![]() . При заданных в системе уравнений
значениях y1 и y2 определяются х1 и х2.
. При заданных в системе уравнений
значениях y1 и y2 определяются х1 и х2.
Пример 3.
Замечание: На практике недостатки методов п.п. 4 и 6, состоящие в больших временных затратах при вычислении определителя матрицы и нахождения обратной матрицы систем с большим числом уравнений и переменных, приводят к их ограниченному использованию.
6. Метод Гаусса
Метод Гаусса применим к решению систем вида А×X = b с любой матрицей А, в том числе и вырожденной или неквадратной.
Метод Гаусса основан на приведении раширенной матрицы (А|b) системы с помощью элементарных преобразований к трапецевидной форме (А1|b1).
Матрице (А1|b1) соответствует линейная система, равносильная исходной, но более простая.
Пример 3. Решить систему методом Гаусса:
1) 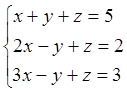
(А|b)=![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() = (А1|b1) – матрица, которой соответствует система
= (А1|b1) – матрица, которой соответствует система 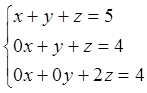 Þ
Þ
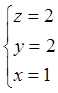 x
= 1, y = 2, z =
2.
x
= 1, y = 2, z =
2.
2) 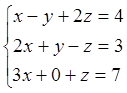 (А|b)=
(А|b)=![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() Þ
(А1|b1| - матрица,
которой соответствует система
Þ
(А1|b1| - матрица,
которой соответствует система 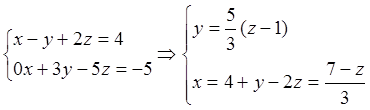
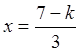 ,
, 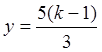 ,
z = k , k – любое число, следовательно система имеет бесчисленное
множество решений и получить решения можно, подставляя вместо k
конкретные числовые значения.
,
z = k , k – любое число, следовательно система имеет бесчисленное
множество решений и получить решения можно, подставляя вместо k
конкретные числовые значения.
3) 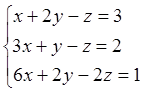 Þ
(A|b)=
Þ
(A|b)=![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() Û
Û![]()
![]()
![]()
![]() = (A1|b1) – матрица, которой соответствует система
= (A1|b1) – матрица, которой соответствует система 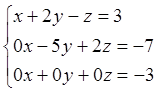 не имеющая решений. Система
несовместна.
не имеющая решений. Система
несовместна.
Замечание: Достоинство метода Гаусса состоит в том, что:
· применим к решению систем вида АX=bс любой матрицей, в том числе и вырожденной и ли неквадратной;
· менее трудоемкий;
· позволяет однозначно установить, совместна система или нет;
· в случае совместности найти решение системы (единственное или бесконечное множество);
· дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
Обобщение материала
Результаты исследования системы могут быть представлены в виде таблицы:
|
|
r=n уравнения системы независимые |
|
Система совместная |
r=n Система определенная (единственное решение) |
|||
|
Система m линейных уравнений с n переменными |
|||||||
|
r<n уравнения системы зависимые |
r(A) ¹ r(A|b) Система несовместная |
r<n Система неопределенная (бесконечное множество решений) |
|||||
|
|
|||||||
|
Решение системы методом Гаусса |
|||||||
Практикум 4
1. Выписать матрицу А и расширенную матрицу (А|b) системы:
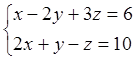
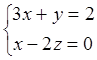
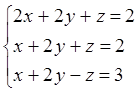
![]()
2. Вычислить обратную матрицу системы и с ее помощью найти решение системы:
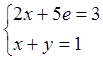
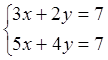
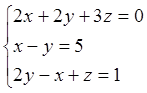
3. Решить систему методом Крамера:
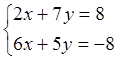
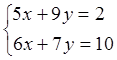
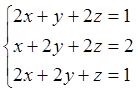 Отв.
(-3;2), (4;-2), (-2/5;3/5;3/5)
Отв.
(-3;2), (4;-2), (-2/5;3/5;3/5)
4. Решить систему методом Гаусса:
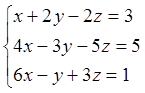
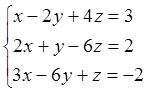
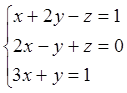 Отв.
(1;2;-1), (3;2;1), (с;1-3с;1-5с)
Отв.
(1;2;-1), (3;2;1), (с;1-3с;1-5с)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.