Уравнение имеет вид: у¢¢ + ру¢ + qy = 0
Алгоритм решения
Для уравнения у¢¢ + ру¢ + qy = 0 составляют характеристическое уравнение l2+pl+q=0.
Пусть l1 и l2 - корни характеристического уравнения тогда возможны три варианта:
10. l1 ¹ l2 , l1, l2ÎR,
тогда общее решение уравнения y=![]() , где С1, и С2 - постоянные.
, где С1, и С2 - постоянные.
20. l1 = l2 , l1ÎR,
тогда общее решение y=![]()
30. l1 = a + ib,
l2 = a -
ib, l1, l2Î C, b ¹
0, тогда общее решение y=![]() Пример 7. Найти общее решение
уравнения у" - 5у + 6у = 0 .
Пример 7. Найти общее решение
уравнения у" - 5у + 6у = 0 .
Характеристическое уравнение l2 - 5l + 6 = 0 имеет корни l1 = 2, l2 = 3,
поэтому (10)общее решение у = С1е2x + C2e3x .
Пример 8. Найти общее решение уравнения у" - 4у¢ + 4у = 0 .
Характеристическое уравнение l2 - 4l + 4 = 0 имеет корни l1 = l2 = 2,
поэтому (20)общее решение у = (С1 + C2 х)e2x .
Пример 9. Найти решение задачи Коши
у¢¢ + 4y = 0, y(0) = 1, y'(0) = 4 .
Характеристическое уравнение l2 +4 = 0 имеет корни l1 = +2i , l2= -2i,
поэтому (30)общее решение у = С1cos 2x + С2 sin 2x .
Используем начальные условия: у(0) = С1 × 1 + С2 × 0 = 1 получаем С1 = 1 .
y'(0) = (-2С1 sin 2x + 2С2 cos 2x)|x=0 = 2С1 × 0 + 2С2 × 1 = 4 => С2 = 2 .
Таким образом, искомое решение задачи Коши имеет вид: у = cos 2x + 2 sin 2x .
Однородное уравнение Эйлера
Уравнение имеет вид: х2у¢¢ + рху¢ + qy = 0
Алгоритм решения
Подстановкой y= xkполучаем аналог характеристического уравнения k×(k - 1) + pk + q = 0
Пусть l1 и l2 - корни характеристического уравнения тогда возможны три варианта:
10. l1 ¹ l2 , l1, l2ÎR,
тогда общее решение уравнения y=![]() , где С1, и С2 - постоянные.
, где С1, и С2 - постоянные.
20. l1 = l2 , l1ÎR,
тогда общее решение y=![]()
30. l1 = a + ib,
l2 = a -
ib, l1, l2Î C, b ¹
0, тогда общее решение y=![]()
Неоднородное уравнение
Алгоритм решения
Уравнение имеет вид у¢¢ + ру¢ + qy = f(x)
Общее решение неоднородного уравнения y(x)= yодн(х) + у*(х) является суммой:
· общего решения yодн(х), соответствующего однородного уравнения у¢¢ + ру¢ + qy = 0, и ·частного решения у*(х) неоднородного уравнения у¢¢ + ру¢ + qy = f(x).
Частное решение уравнения (в простейших случаях) ищут методом неопределенных коэффициентов в виде, определяемом видом функции f(x) и корнями l1, l2 характеристического уравнения l2+pl+q=0.
1°. Пусть f(x) = Рп(х) - многочлен степени п.
·a Если l1 ¹ 0, l2 ¹ 0 , то у* (х) ищут в виде Qn(x), где Qn(x) - многочлен степени п
·b Если l1 ¹ 0, l2 = 0, то y*(x) ищут в виде x×Qn(x).
·c Если l1 = l2 = 0, то y* (x) ищут в виде x2×Qn(x).
2°. Пусть f(x) = aeax, a,a Î R -постоянные.
·a Если l1 ¹a , l2 ¹ a, то у * (х) ищут в виде А × еax .
·b Если l1 = a , l2 ¹a , то у * (х) ищут в виде А × х × еax .
·c Если l1 = l2 = a , то у * (х) ищут в виде А × х2 ×еax .
3°. Пусть f(x) = acosbx + b sinbx, a, b, bÎR - постоянные.
·a Если l1 ¹ ib , l2 ¹ ib , то у*(х) ищут в виде Acosbx + Bsinbх , где А и В постоянные.
·b Если l1= ± ib , то у*(х) ищут в виде x(Acosbx + Bsinbx).
Пример 10. Найти общее решение уравнения у" - 5у' = 7 – 10x.
1.Ищем общее решение yодн (x) соответствующего однородного уравнения у" - 5у' = 0 .
l2 - 5l = 0 Þl1 = 0 l2 = 5 , yодн (x)=C1 + C2e5x
2. Ищем частное решение неоднородного уравнения в виде (1°b) x·Q1(x) , где Q1(x) - многочлен первой степени с неопределенными коэффициентами, у*(х) = х(Ах + В) = Ах2 + Вх.
Найдем первую и вторую производные: (у*(x))¢ = 2Ax +B, (у*(x))¢¢ = 2A
и подставим в исходное уравнение: 2A –10Ax –5B=7 –10x
Сравнивая
коэффициенты, получаем систему: 
Таким образом, частное решение у*(х) = х2 - х
3. Общее решение уравнения у = С1 + С2е5x + х2 - х .
Пример 11. Найти решение задачи Коши у¢¢- 4у¢ + 3у = 2еx, y(0) = 1, у'(0) = 2
1.Ищем общее решение yодн (x) соответствующего однородного уравнения у¢¢- 4у¢ + 3у = 0
l2 - 4l + 3= 0, l1 = 1, l2 = 3Þ yодн (x)=C1ex + C2e3x
2. Ищем частное решение неоднородного уравнения в виде (2°b) у*(х) = Ахeax = Ахex.
Найдем первую и вторую производные:
(у*(x))¢ = Aex +Axex =Aex(x+1),
(у*(x))¢¢ = Aex(x+1)+ Aex = Aex(x+2)
и подставим в исходное уравнение: Aex(x+2) - 4Aex(x+1)+ 3Axex =2ex Þ -2A=2, A= -1.
Таким образом, частное решение у*(х) = -хex.
3. Общее решение уравнения y =C1ex + C2e3x - хex.
4. Для нахождения С1 и С2, используем заданные начальные условия:
y(0)=1=C1+C2
y¢(0)= 2= C1ex+3C2e3x - ex - xex = C1+3C2-1
Получаем
систему: 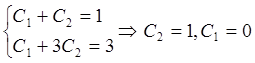
Следовательно, решением задачи Коши является функция у = е3x – хеx
Функция y=j(x,C1,C2,…,Cn) называется общим решением дифференциального уравнения F(x,y,y¢,…,y(n))=0 n-го порядка, существенно зависящая от n произвольных постоянных и обращающая уравнение n-го порядка в тождество при любомх значениях этих постоянных.
Частными решениями, называются решения, получаемые из общего решения при закреплении постоянных C1,C2,…,Cn ,.
Пример 12. Найти решение диффренциального
уравнения 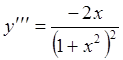 , у которого
, у которого
![]() ,
, ![]() ,
,
![]() .
.
Интегрируя, найдем 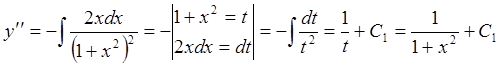 ,
,
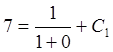 , С1=6
, С1=6
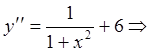
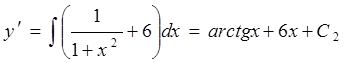
![]()
![]()
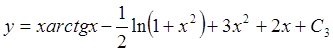
![]()
![]() и
и 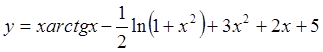 .
.
Уравнение в полных дифференциалах имеет вид P(x,y)dx+Q(x,y)dy=0, левая часть которого есть полный дифференциал.
Для решения этого уравнения надо найти первообразную F(x,y) левой части уравнения. Тогда равенство F(x,y)=C будет общим интегралом нашего дифференциального уравнения.
Пример 12. Найти общий интеграл уравнения (3x2y+y2)dx+(x3+2xy+10y)dy=0
Здесь P=3x2y+y2, Q=x3+2xy+10y, значит 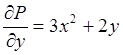 ,
, 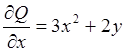 ,
, 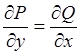
Первообразная имеет вид F(x,y) = ò(3x2y + y2)dx = x3y + xy2+ j(y), где j(y) находится из условия F¢y(x,y) = Q Þ x3+2xy+j(y)¢ = x3+2xy+10y, отсюда j(y)¢ = 10y и j(y)=5y2+C.
Так как нас интересует какая- нибудь одна первообразная, то положив С=0, получим:
F(x,y) = x3y + xy2+5y2, поэтому общий интеграл есть x3y + xy2+5y2 = С.
Разностные методы решения обыкновенных дифференциальных уравнений
Разностные методы решения дифференциальных уравнений - это способы вычисления значений искомого решения у (х) на некоторой сетке значений аргумента.
Разностные методы позволяют находить только конкретное (частное) решение, например решение задачи Коши. Эти методы являются основными при решении дифференциальных уравнений с помощью ЭВМ.
Метод Эйлера (метод ломаных)
Этот метод дает хорошее приближение к решению только для достаточно малых hn.
Пусть требуется решить задачу Коши для уравнения первого порядка y¢ =f(x,y), y(x0)=y0 I
На данном
отрезке выбирают некоторую сетку значений агумента х0, x1, .... xn, для которых вычисляют
значения функции у по схеме: yn+1 = yn + hn f(xn,
уn),
h = хn+1 -
хn,
где n = 0, 1, ..., n-1.
Модификации этого метода определяются
следующими формулами:
yn+1 = yn + hn f 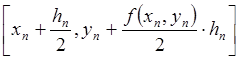
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.