yn+1 = yn + ![]() {f(xn,
уn)+
f[xn+1,yn + f(xn,yn) hn]}
{f(xn,
уn)+
f[xn+1,yn + f(xn,yn) hn]}
Метод Рунге - Кутта
Обеспечивает более высокую точность.
Наиболее употребительной является следующая схема:
yn+1 = yn + ![]() (k1+2k2+2k3+k4),
где
(k1+2k2+2k3+k4),
где
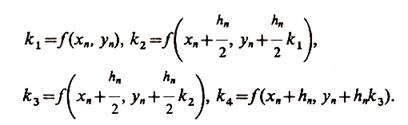
Пример 13.
Решить задачу Коши методом Рунге - Кутта для дифференциального уравнения у' = х2 + у2, у(0)=1 на отрезке [0;0,7].
Выберем шаг h = 0,1. Используя формулу, получаем следущие значения функции у на сетке значений х:
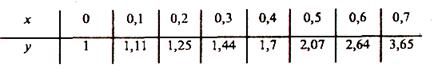
Пусть дано дифференциальное уравнение y¢ = f(x,y), частное решение которого
удовлетворяет
начальным условием ![]() .
.
Найдем значение y1 интересующего нас решения в точке x1, весьма близкой к x0.
Поскольку значение y1, отвечающее значению x0, нам известно, то задача сводится к нахождению приращения y1 – y0 =Dу , вызванного приращением Dx = xl – х0 .
При малом приращении Dx с большой точностью Dу представимодифференциаломdy = y¢Dx ,
тогда можно записать Dу @ y¢Dx=f¢(x0,y0)Dx изаменяя y1 – y0 = Dу и Dx = xl – х0 , находим:
y1 @ y0 + f¢(x0,y0)(x - x0)
Это основная расчетная формула метода Эйлера — Коши.
Ее точность тем выше, чем меньше разность xl – х0.
Пример 13.
Пусть у=у(х)
- то решение дифференциального уравнения 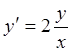 ,
которое удовлетворяет условию
,
которое удовлетворяет условию ![]() .
.
1) Найдем y|x=2=?.
Так как промежуток от x =1 до х = 2 не может считаться малым, то мы разделим его на 10 равных частей точками x1 =1,1, x2 = l,2, ... т.е. Dx = 0,1
Тогда в
соответствии с формулой метода Эйлера-Коши, запишем: 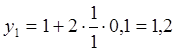 ,
y1-y =0,2
,
y1-y =0,2
y2 =1,2+2×![]() ×0,1=
1,418, y2-y1 = 0,218; и т.д.
×0,1=
1,418, y2-y1 = 0,218; и т.д.
Аналогично находятся остальные значения функции у (х), причем вычисления удобно расположить в следующую таблицу, строение которой не потребует других пояснений, кроме указания, что за Dy принято у' Dx:
|
x |
y |
y¢ |
Dy |
x |
y |
y¢ |
Dy |
|
|
1 |
1 |
2 |
0,2 |
1,6 |
2,472 |
3,09 |
0,309 |
|
|
1,1 |
1,2 |
2,18 |
0,218 |
1,7 |
2,781 |
3,27 |
0,327 |
|
|
1,2 |
1,418 |
2,36 |
0,236 |
1,8 |
3,108 |
3,45 |
0,345 |
|
|
1,3 |
1,654 |
2,54 |
0,254 |
1,9 |
3,453 |
3,63 |
0,363 |
|
|
1,4 |
1,908 |
2,73 |
0,273 |
2 |
3,816 |
|||
|
1,5 |
2,181 |
2,91 |
0,291 |
Эта таблица показывает, что y(2) = 3,816.
2) Исходное уравнение легко решается отделением переменных: 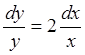
![]() ,
откуда y =Cx2. Чтобы удовлетворить условию y(x=1)=1, надо взять С=1.
,
откуда y =Cx2. Чтобы удовлетворить условию y(x=1)=1, надо взять С=1.
Частное решение есть у= х2.
Точное значение величин y(2) = 4.
Абсолютная ошибка равна 0,184 ( табличное значение у(2) = 3,816 и 4,0 – 3,816=0,184).
Относительная ошибка d = 0,184/4 = 0,046 = 4,6%.
Пример 14. Найти функцию z = z(x,y), удовлетворяющую дифференциальному уравнению 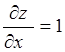
Интегрируя, получим z = x + j(y), где j(y) – произвольная функция – общее решение.
Пример 15. Решить уравнение 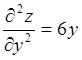 , z = z(x,y)
, z = z(x,y)
Дважды интегрируя по y, получаем 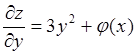 ,
, ![]() ,
где j(х) и w(х) – произвольные функции.
,
где j(х) и w(х) – произвольные функции.
Пример 16. Решить уравнение 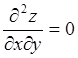
Интегрируя по x, получаем 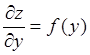
Проинтегрировав полученный результат по y, получим z=j(x)+ w(y), где w(y)=ò f(y)dy
Рассмотрим
дифференциальное уравнение  , где X, Y и Z – функции x, y и z.
, где X, Y и Z – функции x, y и z.
Аргоритм решения
1. Предварительно решим систему обыкновенных дифференциальных уравнений:
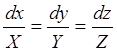
Пусть решение этой системы определяется равенствами:
w1(x, y, z) = C1 и w2(x, y, z) = C2
2. Найдем общий интеграл заданного дифференциального уравнения:
F[w1(x, y, z), w2(x, y, z)] = 0
где F(w1, w2) – произвольная непрерывно дифференцируемая функция.
Пример 17. Найти общий интеграл уравнения 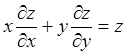
1. Решим систему обыкновенных
дифференциальных уравнений: 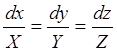
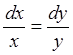 Þ
Þ 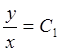 ,
,  Þ
Þ 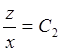
2. Найдем общий интеграл заданного дифференциального уравнения:
F(y/x, z/x) = 0, или z/x =j(y/x), z = x×j(y/x).
где j(y/x), – произвольная функция.
Пример 18. Найти общий интеграл уравнения 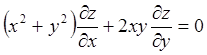
1. Решим
систему обыкновенных дифференциальных уравнений 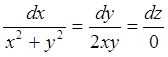 ,
,
применив свойство пропорции,
запишем  или
или 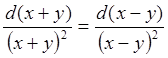 ,
,
2. Интегрируя, получаем: 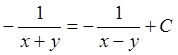 ,
,
 .
.
Второе уравнение системы: dz =0 Þ z =C2.
Общий интеграл имеет вид: 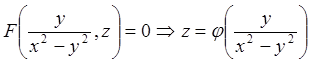 .
.
3. Уравнения второго порядка в частных производных
Рассмотрим уравнение второго порядка
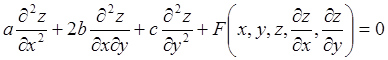
где а, b, с—функции х и у.
Говорят, что указанное уравнение в области D принадлежит:
¨ гиперболическому типу, если в этой области b2—ас > 0;
¨ параболическому типу, если в этой области b2—ас = 0;
¨ эллиптическому типу, если в этой области b2—ас <0;
Уравнения:
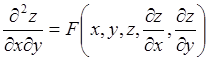 - каноническое уравнение
гиперболического типа;
- каноническое уравнение
гиперболического типа;
 - каноническое уравнение
параболического типа;
- каноническое уравнение
параболического типа; 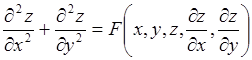 -
каноническое уравнение эллиптического типа.
-
каноническое уравнение эллиптического типа.
Дифференциальное уравнение а (dy)2 – 2b dxdy + с (dx)2=0 называется уравнением характеристик уравнения второго порядка в частных производных.
· Для уравнения гиперболического типа уравнение характеристик имеет два интеграла
j(х, y) = C1, y(x, y) = C2, т. е. существуют два семейства действительных характеристик.
С помощью замены переменных x= j(х, у), h=y (х, у) дифференциальное уравнение второго порядка в частных производных приводится к каноническому виду.
· Для уравнения параболического типа уравнение характеристик имеет один интеграл j(х, у) = С1,2 , т.е. оба семейства характеристик совпадают.
С помощью замены переменных x=j(х, у), h=y (x, у), [где y(х,у) - какая-нибудь функция,
для
которой 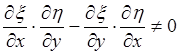 ],
дифференциальное уравнение второго порядка в
частных
],
дифференциальное уравнение второго порядка в
частных
производных приводится к каноническому виду.
· Для уравнения эллиптического типа интегралы уравнения характеристик имеют вид
j(х, у) ± iy(х, y)=C1,2 ,[ где j (х, у) и y(х, y)- действительные функции].
С помощью подстановки x= j(x, у), h = y(x, у) дифференциальное уравнение второго порядка в частных производных приводится к каноническому виду.
Пример
19. Привести к каноническому виду
уравнение 
1. а = х2, b = 0, с = - у2, b2 - ас = х2у2 > 0, т.е. это уравнение гиперболического типа.
2. Составляем уравнение характеристик: x2 (dy)2 – у2 (dх)2 = 0, или (xdy+y dx)×(xdy-y dx) = 0. Получаем два дифференциальных уравнения: xdy+y dx=0 и xdy-y dx=0
3. Разделяя переменные
и интегрируя, имеем 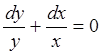 ,
, ![]() Þ xy=C1 и
Þ xy=C1 и 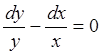 ,
, ![]() Þ
Þ  , тогда xy=C1 и
, тогда xy=C1 и  -
уравнения двух семейств характеристик.
-
уравнения двух семейств характеристик.
4. Введем новые переменные x = xy, h = y/x. Выразим частные производные по старым переменным через частные производные по новым переменным:
![]()
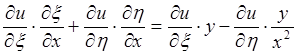
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.