Расчет стержневых систем на устойчивость и динамические воздействия

Расчет стержневых систем на устойчивость и динамические воздействия

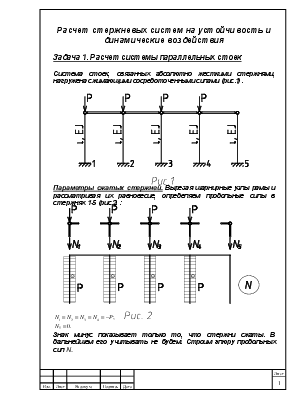
Задача 1. Расчет системы параллельных стоек

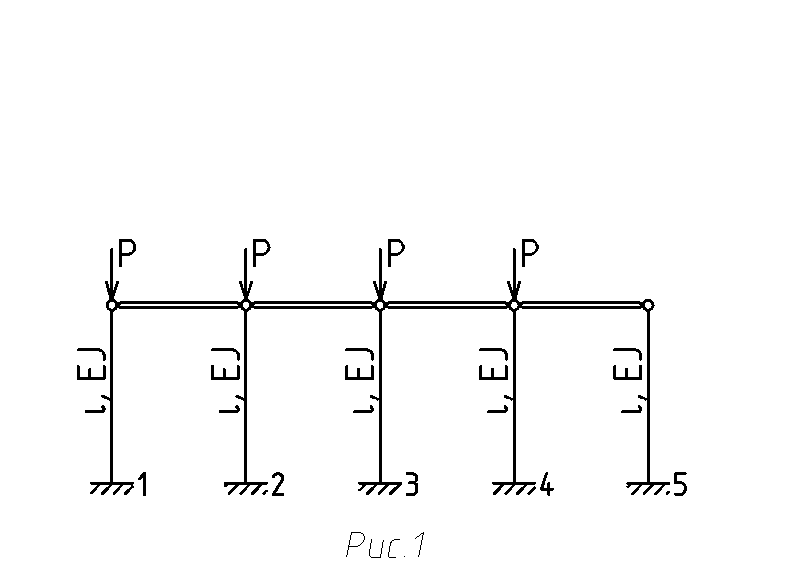
Система стоек, связанных абсолютно жесткими стержнями, нагружена сжимающими сосредоточенными силами (рис.1).

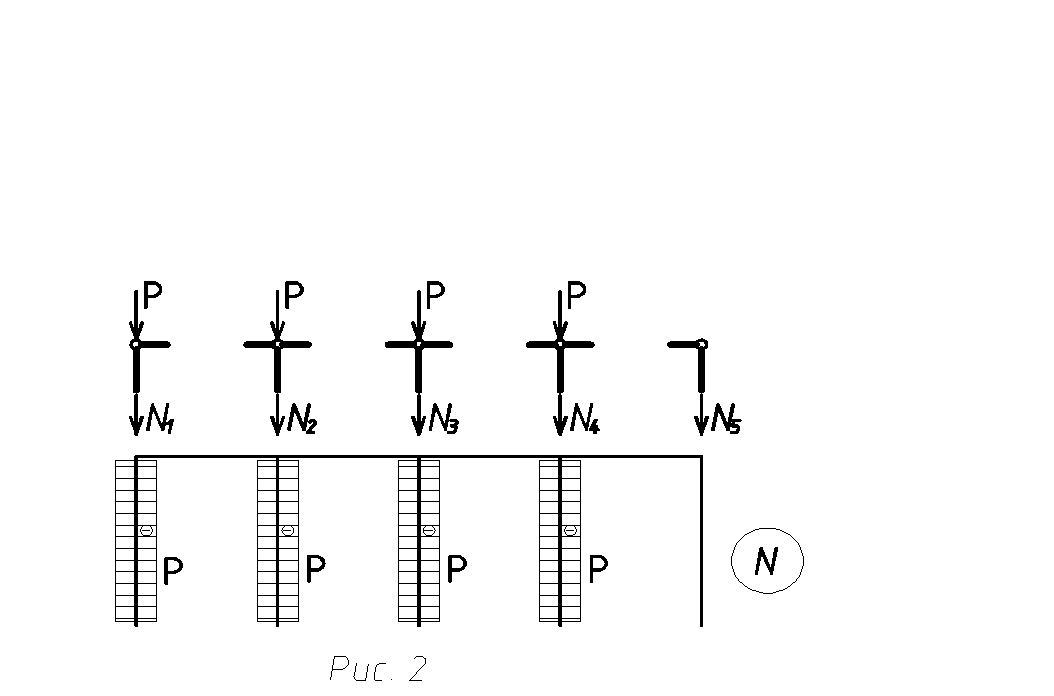
Параметры сжатых стержней.Вырезая шарнирные узлы рамы и рассматривая их равновесие, определяем продольные силы в стержнях 1-5 (рис.2):

Знак минус показывает только то, что стержни сжаты. В дальнейшем его учитывать не будем. Строим эпюру продольных сил N.

Для каждого из стержней определяем :

- для сжатых стоек

- для ненагруженных стоек

Расчеты на устойчивость будем вести методом перемещений.

Степень кинематической неопределимости.

( т.к. нет жестких узлов;  т.к. допускается линейное перемещение узлов по горизонтали).

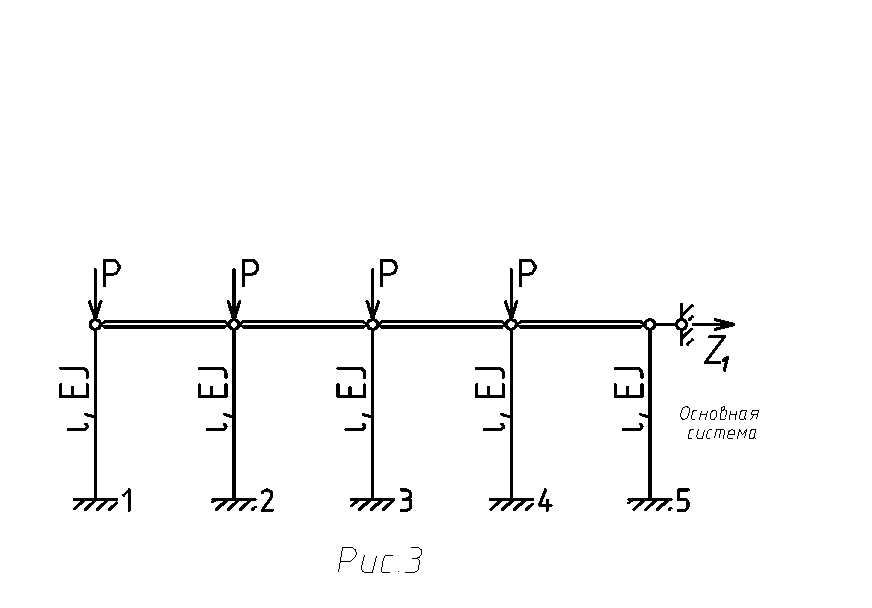
Формирование основной системы. Вводим горизонтальный опорный стержень. Для компенсации введения дополнительной связи основной системе придаем горизонтальное перемещение  (рис.3).

Каноническое уравнение метода перемещений. Так как  будет одно каноническое уравнение:

где  - горизонтальное перемещение, возникающее только при потере устойчивости;  - единичная реакция введенной связи от

Вычисление единичной реакции. Рассмотрим деформирование основной системы в результате перемещения введенной связи на  (рис.4). Чтобы найти реакцию  в горизонтальном стержне, необходимо рассечь этот стержень, а также отсечь раму от опор; в полученных сечениях ввести усилия и составить уравнение проекций всех сил на горизонтальную ось.

В местах сечений прикладываем реакции, взятые из таблиц (для изогнутых стоек 2, 4 – из строки 2 таблицы 1, для сжато-изогнутых стоек 1, 3, 5 – из строки 2 таблицы 2).

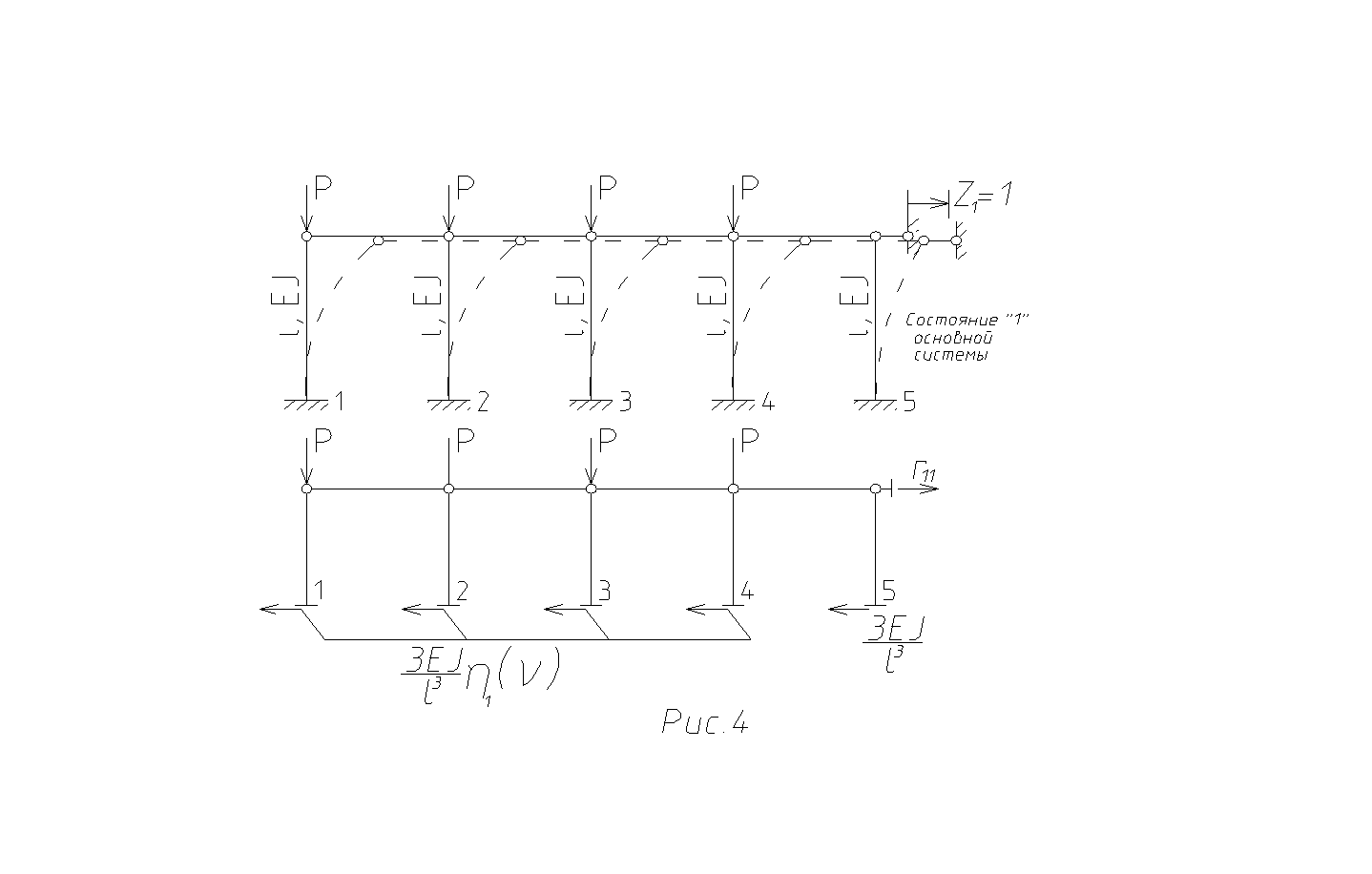
Составляем уравнение проекций всех сил на горизонтальную ось:

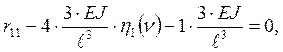
отсюда      

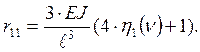
Условие потери устойчивости. Если нагрузка не достигла критической величины, то конфигурация рамы остается той же, что и до приложения нагрузки. Ее стержни испытывают только сжатие, узлы не перемещаются,

С ростом нагрузки увеличиваются продольные силы в сжатых стержнях, а, следовательно, и параметр  Когда сила достигает критического значения сжатые стержни теряют устойчивость, узлы рамы смещаются по горизонтали; возникают качественно новые деформации (деформации изгиба). При этом параметр  также становится критическим ().

Условие потери устойчивости, т.е. ненулевое перемещение

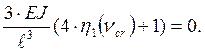
Уравнение устойчивости и его решение.

По таблице функций Смирнова (таблица 3) находим

С помощью линейной интерполяции находим значения критического параметра:

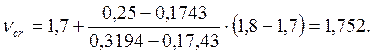
Критическая сила.

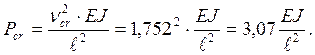
Коэффициент приведения длины сжатых стоек.

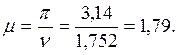
Задача 2. Расчет рамы на устойчивость

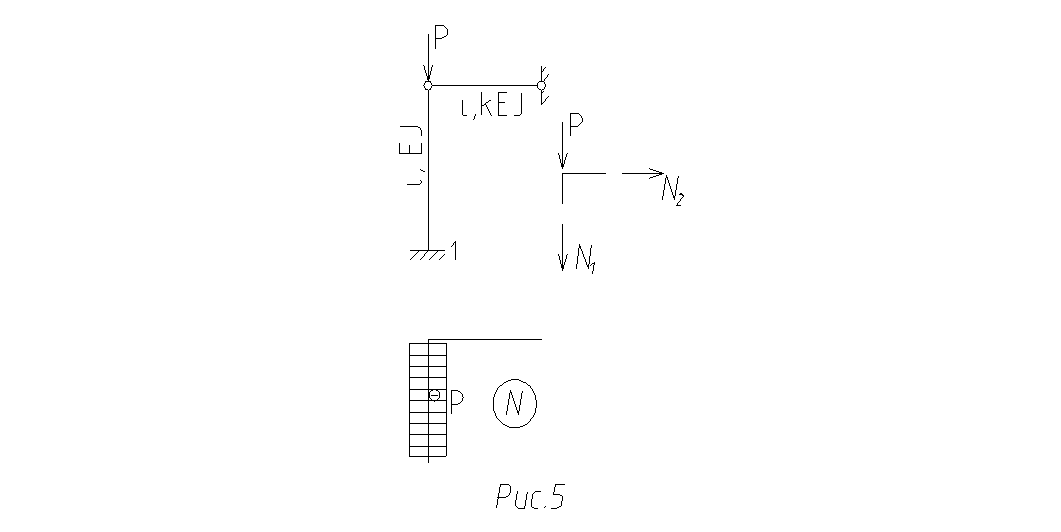
Рама нагружена сосредоточенной силой (рис.5). Жесткость стойки  ригеля - (), их длины одинаковы.

Параметр сжатого стержня. Вырезая узел рамы и рассматривая его равновесие, определяем продольные силы в стержнях:

Знак минус показывает только то, что стержень сжат. В дальнейшем его учитывать не будем. Строим эпюру продольных сил

Параметры :

- для сжатой стойки

- для ригеля

Степень кинематической неопределимости

( т.к. один жесткий узел;  т.к. линейных перемещений узла нет).

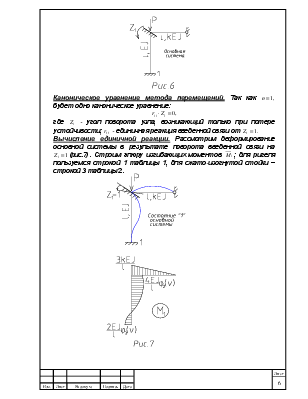
Формирование основной системы. Вводим лавающую заделку в жесткий узел и задаем угол поворота жесткого узла (рис.6).

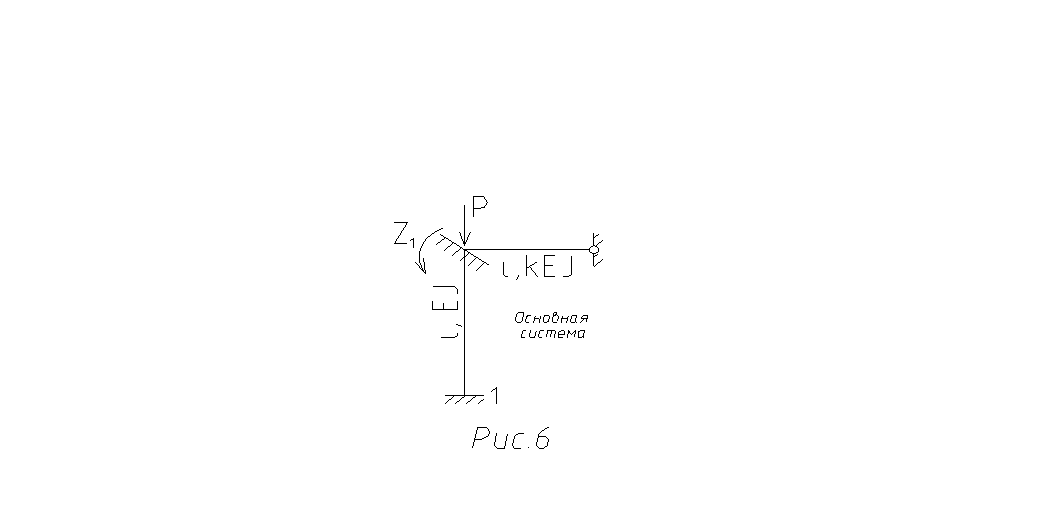
Каноническое уравнение метода перемещений. Так как  будет одно каноническое уравнение:

где  - угол поворота узла, возникающий только при потере устойчивости;  - единичная реакция введенной связи от

Вычисление единичной реакции. Рассмотрим деформирование основной системы в результате поворота введенной связи на (рис.7). Строим эпюру изгибающих моментов ; для ригеля пользуемся строкой 1 таблицы 1, для сжато-изогнутой стойки – строкой 3 таблицы 2.

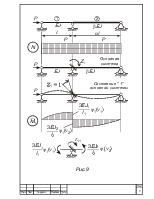
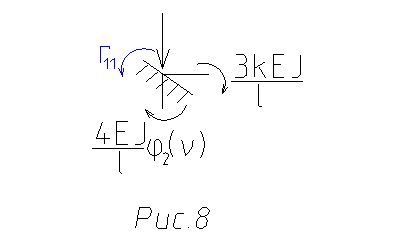Чтобы найти реакцию  в плавающей заделке, необходимо вырезать узел (рис.8); в полученных сечениях ввести моменты и составить уравнения моментов узла:

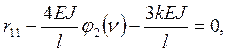 отсюда (при )

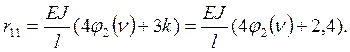
Условие потери устойчивости. Когда сила Р достигает критического значения , сжатая стойка теряет устойчивость, узел рамы поворачивается; возникают деформации изгиба. При этом параметр  становиться критическим

Условие потери устойчивости, т.е. ненулевое перемещение

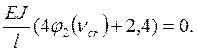
Уравнение устойчивости и его решение.

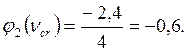
По таблице функций Смирнова (таблица 3) находим

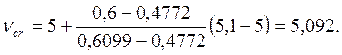
Критическая сила.

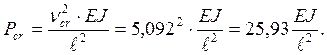
Коэффициент приведения длины сжатой стойки.

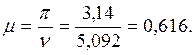
Задача 3. Расчет неразрезного стержня

Стержень переменной жесткости, имеющий промежуточную опору (неразрезной стержень) нагружен вдоль оси сжимающей силой (рис.9). Жесткость 1-го участка EJ, 2-го участка  , их длины соответственно равны  и  .

Параметр сжатых стержней. Определяем продольные силы на 1-м и 2-м участках:

Знак минус показывает только то, что стержень сжат. В дальнейшем его учитывать не будем. Строим эпюру продольных сил

Параметры :