Расчет стержневых систем на устойчивость и динамические воздействия, страница 2

- для сжатой стойки

- для ригеля

Степень кинематической неопределимости

( т.к. один жесткий узел;  т.к. линейных перемещений узла нет).

Формирование основной системы. Вводим плавающую заделку в жесткий узел и задаем угол поворота жесткого узла (рис.6).

Каноническое уравнение метода перемещений. Так как  будет одно каноническое уравнение:

где  - угол поворота узла, возникающий только при потере устойчивости;  - единичная реакция введенной связи от

Вычисление единичной реакции. Рассмотрим деформирование основной системы в результате поворота введенной связи на (рис.9). Строим эпюру изгибающих моментов ; пользуемся строкой 1 таблицы 2.

 Чтобы найти реакцию  в плавающей заделке, необходимо вырезать узел (рис.8); в полученных сечениях ввести моменты и составить уравнения моментов узла:

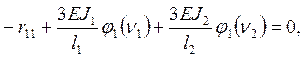 отсюда (при )

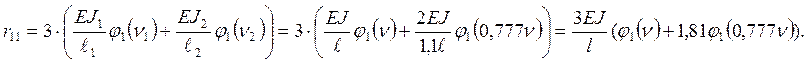
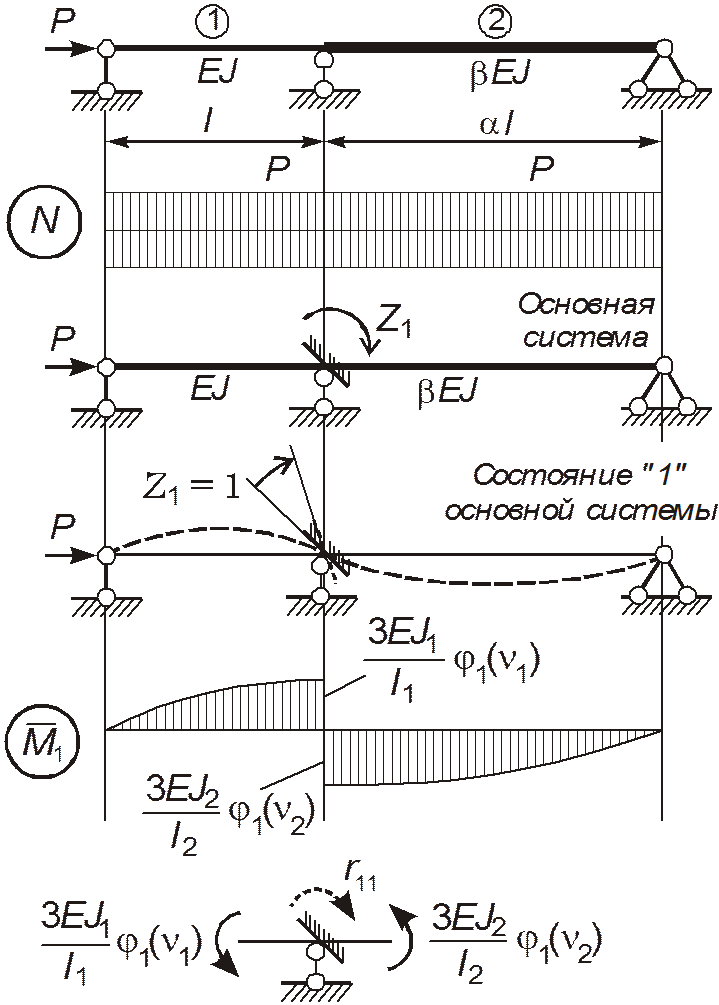
Рис.9

Условие потери устойчивости. Когда сила Р достигает критического значения , неразрезной стержень теряет устойчивость, возникает деформации изгиба , сечение над опорой поворачивается.. При этом параметр  становиться критическим

Условие потери устойчивости, т.е. ненулевое перемещение

   

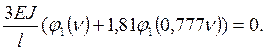
Уравнение устойчивости и его решение.

Решение ищем путем подбора, пользуясь таблицей 3. Обозначим

Для наглядности процесс подбора поясняем графиком (рис.10).

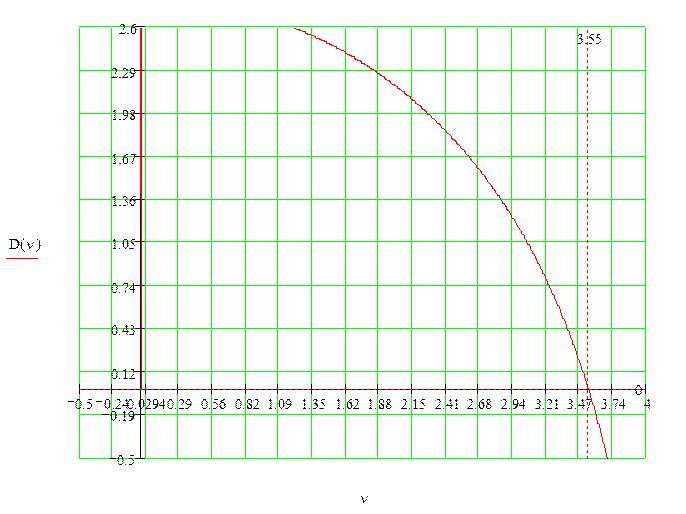
Рис.10

Следовательно, критическое значение параметра

Для 1-го участка ,

Для2-го участка

Критическое значение внешней силы.

Для 1-го участка ,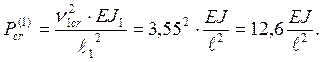

Для2-го участка

 Критическая сила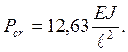

Задача 4. Расчет системы с двумя степенями свободы на свободные колебания

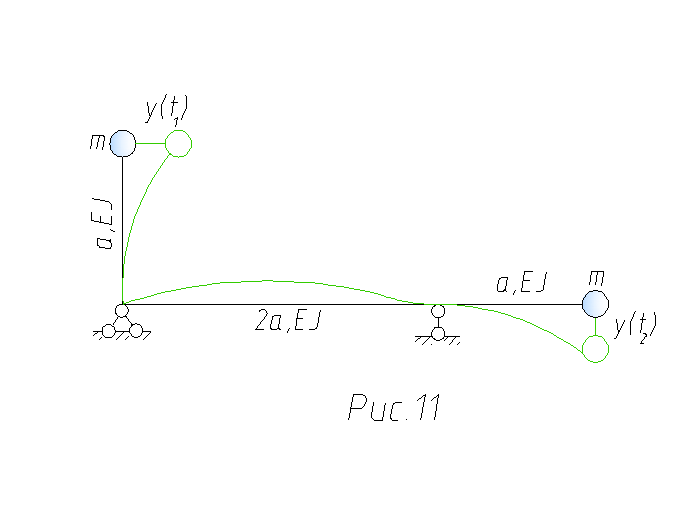Исходные данные: масса каждого из точечных грузов  длины участков жесткость стержней системы Заданная система представлена на (рис.11).

Число степеней свободы. Движение из плоскости чертежа считаем невозможным. Вращением грузов пренебрегаем. В соответствии с гипотезой о малости перемещений каждый груз может совершать перемещения только в одном направлении – по перпендикуляру к недеформированной оси рамы. Поэтому система обладает двумя степенями свободы. Перемещение грузов обозначим  (см.рис.9).

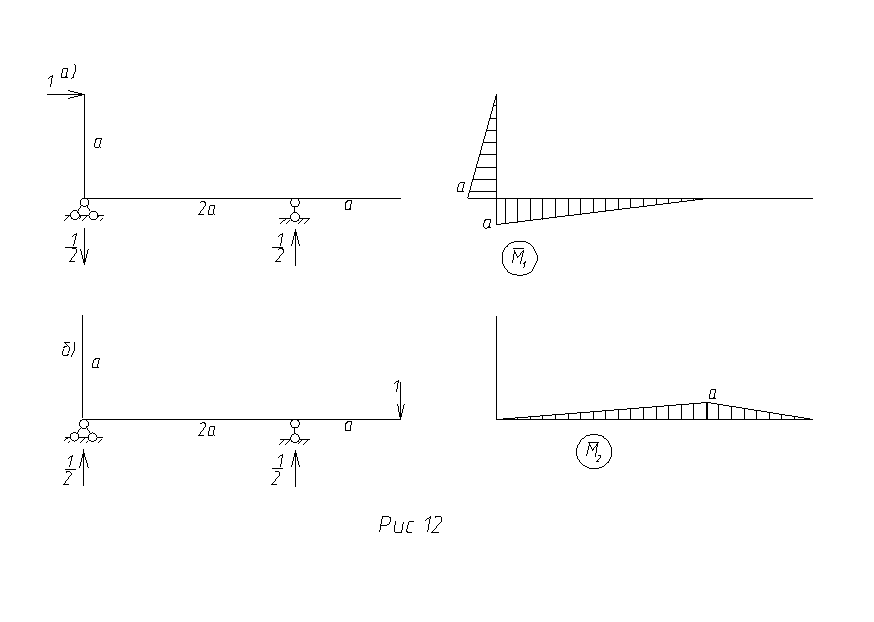
Определение единичных перемещений. В направлении  прикладываем горизонтальную единичную силу и строим эпюру  (рис.12,а). В направлении  прикладываем вертикальную единичную силу и строим эпюру  (рис.12,б).

Для вычисления перемещений используем формулу Мора:

 

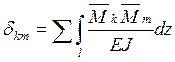
где - перемещения по направлению  от действия единичного усилия, приложенного по направлению

Единичные перемещения  называют главными, они всегда положительны;  - побочные единичные перемещения, в соответствии с теоремой Максвелла  Все стержни прямолинейны, их жесткость постоянна. Для перемножения эпюр воспользуемся способом Симпсона.

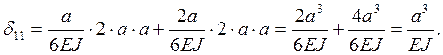
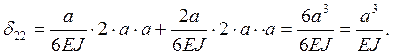
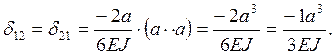
Система уравнений движения.

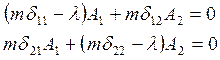  или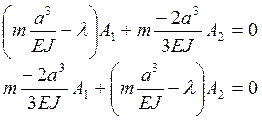  

где - собственные числа.

Упрощаем систему, умножая на 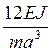 и вводя обозначения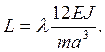

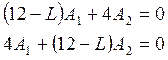          (1)

Это однородная система линейных алгебраических уравнений относительно амплитуд  Она имеет ненулевое решение, если ее определитель равен нулю, то есть:

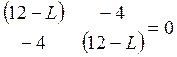       (2)

Характеристическое уравнение и его решение. Раскрывая определитель (2), получим характеристическое уравнение:

или

Дискриминант  Корни

  

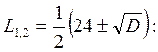
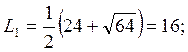
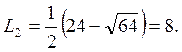
(Корни нумеруем так, чтобы выполнялось условие ).

Частоты колебаний.Собственные числа и частоты колебаний связаны соотношением  С учетом обозначения L, введенного в (1), получаем

  

                

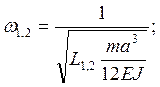
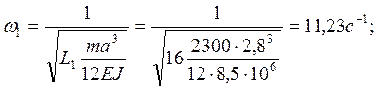
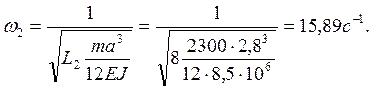
(Частоты должны быть пронумерованы так, чтобы ).

Формы колебаний. Первая форма колебаний соответствует частоте ,  В системе (1) к  добавляем индекс «1»:

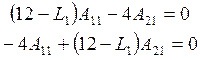   (3)

Задаемся значением амплитуд  Подставляем  и  в (3). Неизвестна всего одна амплитуда  для определения которой можно использовать любое уравнение системы (3), например, первое:

        

- амплитудное значение перемещения  при колебаниях с частотой ; - амплитудное значение перемещения  при колебаниях с частотой .

Вторая форма колебаний соответствует частоте ,  В системе (1) к  добавляем индекс «2»:

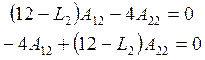   (4)

Задаемся значением амплитуд  Подставляем  и  в (4). Неизвестна всего одна амплитуда  для определения которой второе уравнение системы (4):

        

- амплитудное значение перемещения  при колебаниях с частотой ; - амплитудное значение перемещения  при колебаниях с частотой .

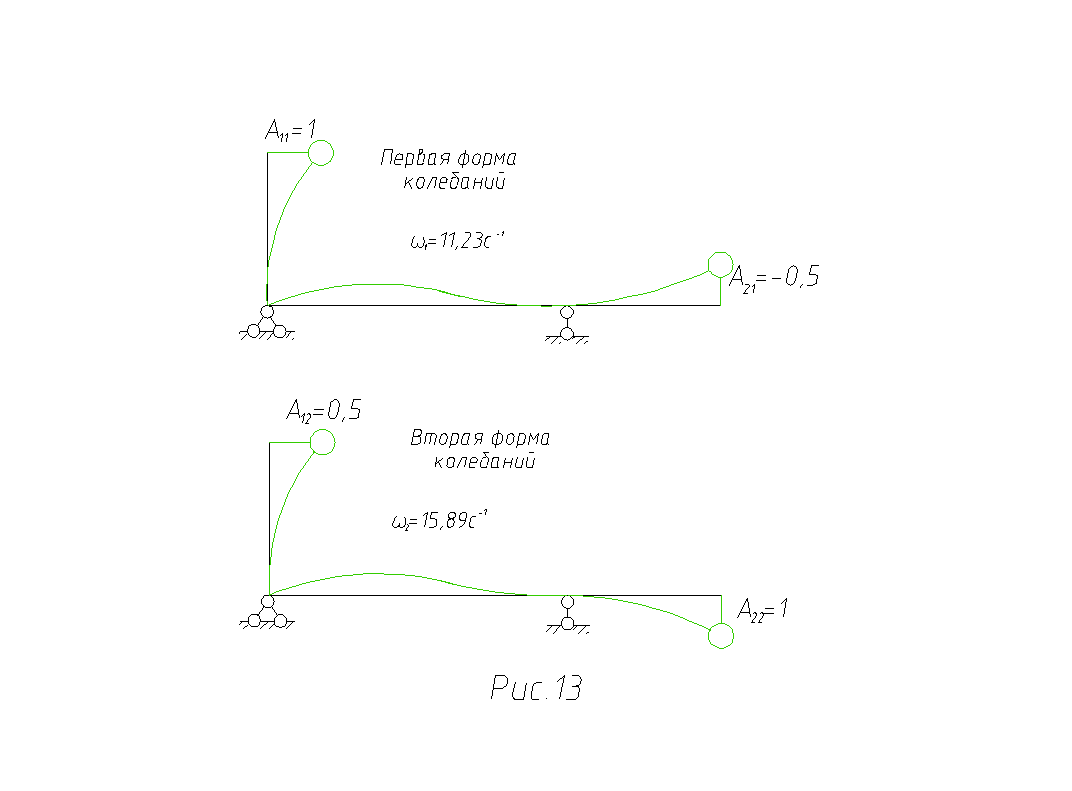Показываем формы колебаний (рис.13). Положительные амплитуды откладываем в направлениях, совпадающих с направлениями перемещений , отрицательные – противоположно.

Проверка ортогональности форм колебаний. Для рассматриваемой системы с двумя степенями свободы, у которой массы точечных грузов одинаковы, должно выполняться условие:

Подставляя значения амплитуд, получим

Проверка выполняется.

Литература

1.  Конспект лекций по строительной механике;

2.  Пример расчета стержневых систем на устойчивость и динамические воздействия, А.В. Яровая;