Пример расчета рамы методом сил

Пример расчета рамы методом сил

Расчетная схема рамы показана на рисунке 1. Требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

1 Степень статической неопределимости. Мысленно соединив опоры рамы, получим один замкнутый контур (К = 1), содержащий два шарнира (Ш = 2). Следовательно .

2 Основная система. Отбрасываем вертикальный опорный стержень и заменяем его реакцией  (рисунок 2).

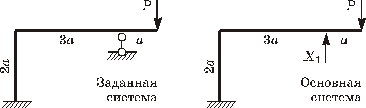
Рисунок 1                           Рисунок 2

3 Каноническое уравнение. Так как s = 1, составляем одно уравнение

, где  – единичное и грузовое перемещения в основной системе.

4 Единичная и грузовая эпюры в основной системе.

Формируем состояние «1» основной системы, прикладывая к ней единичную силу по направлению . Строим единичную эпюру  Далее формируем состояние «p» основной системы, прикладывая к ней внешнюю нагрузку. Строим грузовую эпюру  (рисунок 3).

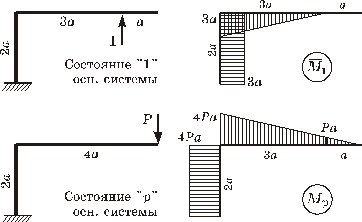
Рисунок 3

5 Вычисление единичного и грузового перемещений. В соответствии с методом Мора

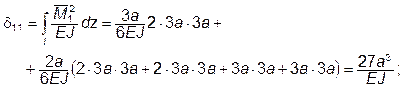
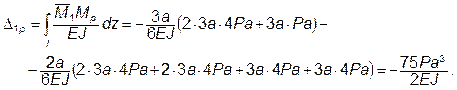
При перемножении соответствующих эпюр мы пользовались способом Симпсона для прямолинейных эпюр.

6 Решение канонического уравнения. Из канонического уравнения выражаем неизвестную силу:

.

7 Построение эпюры изгибающих моментов M. На основании принципа суперпозиции

.

Строим эпюру , умножая ординаты эпюры  на  (рисунок 4), и складываем ее с . Получаем эпюру изгибающих моментов M в заданной системе (рисунок 5).

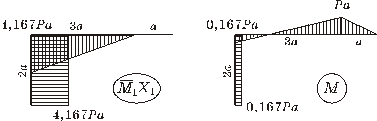
Рисунок 4                              Рисунок 5

8 Проверка эпюры M. Выполняем деформационную проверку, умножая по методу Мора эпюру M на единичную эпюру :

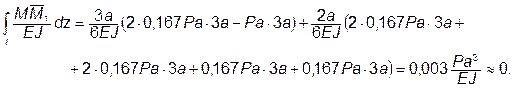
Проверка выполняется.

9 Построение эпюр Q, N. Выполняем построения в статически определимой основной системе, приложив к ней известную силу  (рисунок 6).

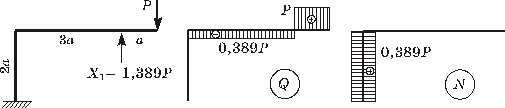
Рисунок 6

Таким образом, расчет рамы выполнен.

Пример расчета рамы методом перемещений

Расчетная схема рамы показана на рисунке 1. Требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

1 Степень кинематической неопределимости. Рама имеет один жесткий узел, поэтому количество независимых угловых перемещений . Образуем шарнирную схему (рисунок 2). Мысленно соединим ее опоры – получим один замкнутый контур (К = 1), содержащий три шарнира (Ш = 3). Следовательно, количество независимых линейных перемещений . Степень кинематической неопределимости .

2 Основная система. Вводим дополнительную связь – плавающую заделку в жесткий узел и задаем ей угловое перемещение (рисунок 3).

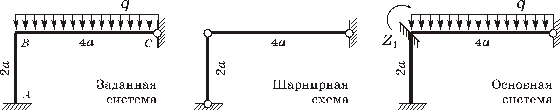
Рисунок 1                    Рисунок 2                  Рисунок 3

3 Каноническое уравнение. Так как , составляем одно уравнение

, где  – единичная и грузовая реакции введенной связи.

4 Единичная и грузовая эпюры в основной системе.

Формируем состояние «1» основной системы, задавая поворот плавающей заделки на единичный угол в направлении . Пользуясь таблицей, строим единичную эпюру  Далее формируем состояние «p» основной системы, прикладывая к ней внешнюю нагрузку. Строим грузовую эпюру  (рисунок 4).

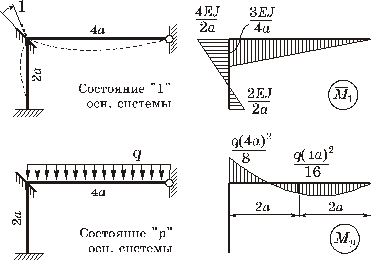
Рисунок 4

5 Вычисление единичной и грузовой реакций. В соответствии со статическим методом определения реакций вырезаем жесткий узел и рассматриваем его равновесие в двух состояниях – единичном и грузовом (рисунок 5). Составляя уравнение моментов, находим реакции:

Рисунок 5

6 Решение канонического уравнения. Из канонического уравнения выражаем неизвестное перемещение:

.

7 Построение эпюры изгибающих моментов M. На основании принципа суперпозиции

.

Строим эпюру , умножая ординаты  на  (рисунок 6), и складываем ее с . Получаем эпюру изгибающих моментов M в заданной системе (рисунок 7).

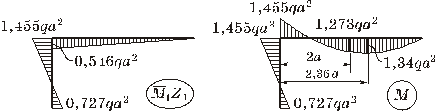
Рисунок 6                              Рисунок 7

8 Проверка эпюры M. Выполняем статическую проверку равновесия узла (рисунок 8):   Проверка выполняется.

Рисунок 8

9 Построение эпюры Q. Эпюру поперечных сил строим по готовой эпюре М. На участке AB (см. рисунок 1), используя дифференциальную зависимость Q от M, получаем

.

Участок BC рассматриваем отдельно, приложив к его сечениям искомые силы  и момент , взятый из эпюры М (рисунок 9, а). Составив уравнения моментов относительно точек С и В, получаем:

;

.

Строим эпюру Q (рисунок 10).

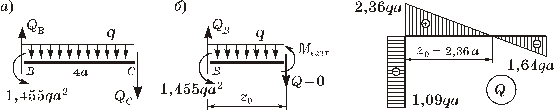
Рисунок 9                                                 Рисунок 10

В сечении, где эпюра Q пересекла ось на участке BC, момент будет иметь экстремальное значение. Определим расстояние  из условия равенства нулю поперечной силы в данном сечении (рисунок 9, б):

;   .

Экстремальный момент

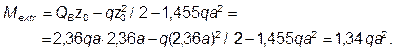
Отмечаем это значение на эпюре М (см. рисунок 7).

10 Построение эпюры N. Вырезаем жесткий узел (рисунок 11), прикладываем к его сечениям поперечные силы Q с учетом знака (положительная сила совершает вращение по часовой стрелке), а также искомые продольные силы N (от сечения в сторону отброшенной части). Из условий равновесия

Строим эпюру N (рисунок 12).

Рисунок 11                         Рисунок 12

11 Проверка равновесия рамы. Отсекаем раму от опор и в полученных сечениях прикладываем моменты и силы, взятые из эпюр M, Q, N (рисунок 13). Составляем уравнения равновесия:

Рисунок 13

Рама в равновесии, следовательно, расчет выполнен верно.