





Этот метод впервые был предложен венгерским математиком Эгервари в 1931 году и длительное время оставался малоизвестным. В 1953 году математик Г. Кун перевёл работу на английский язык и несколько усовершенствовал венгерский метод.
Введём ряд определений:
1 Задачи линейного программирования называются эквивалентными, если их оптимизирующие наборы совпадают.
2 Преобразование, переводящее задачу линейного программирования в эквивалентную ей, будем называть эквивалентным.
3 Систему нулевых элементов матрицы, обладающую тем свойством, что никакая пара из них не лежит в одной строке или в одном столбце, будем называть системой независимых нулей.
Алгоритм венгерского метода состоит в преобразовании исходной задачи линейного программирования в эквивалентную ей задачу минимизации, матрица C=(сij), (i=1,…,n; j=1. ,n) которой содержит неотрицательные элементы. Если в матрице C имеется система из n независимых нулей, то решением задачи будет матрица X с единичными элементами на местах, соответствующих независимым нулям, и с остальными нулевыми элементами. Алгоритм направлен на построение системы независимых нулей путём эквивалентных преобразований матрицы C.
Алгоритм решения задачи о назначениях Венгерским методом.
Алгоритм этого метода включает четыре основных этапа. Для поиска оптимального решения потребуется не более чем n – 2 последовательно проводимых итераций.
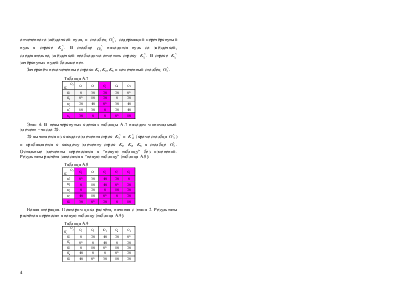
Этап 1. Получение нулей в каждой строке и каждом столбце. Находим наименьший элемент в каждой строке исходной таблицы, вычитаем его из всех её элементов и получаем новую таблицу. Аналогично производим действия для каждого столбца “новой таблицы”. Получаем следующую “новую” таблицу.
Примечание. Если исходная задача ЛП была задачей на максимум, то она должна быть преобразована в задачу минимизации, например, следующим эквивалентным преобразованием матрицы C. Необходим максимальный элемент в каждом столбце исходной таблицы, вычитаем из него все элементы её столбцов и получаем новую таблицу.
Этап 2. Проверка решения на оптимальность. Ищем строку, содержащую наименьшее число нулей, отмечаем звёздочкой один из них и зачёркиваем все остальные нули этой строки и столбца, содержащего нуль со звёздочкой, Аналогичные операции последовательно выполняем для всех строк. Если число нулей, отмеченных звёздочкой, равно n, то решение является оптимальным (задача решена), в противном случае осуществляется переход к следующему этапу.
Этап 3. Поиск минимального набора строк и столбцов, содержащих нули.
Необходимо отметить звёздочкой:
а) все строки, не имеющие ни одного отмеченного нуля;
б) все столбцы, содержащие перечёркнутый нуль хотя бы в одной из отмеченных звёздочкой строк;
в) все строки, содержащие отмеченные звёздочкой нули хотя бы в одном из помеченных столбцов.
Далее повторяются поочерёдно действия б) и в) до тех пор, пока есть, что отмечать.
После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец. Цель этого этапа – провести минимальное число горизонтальных и вертикальных прямых, пересекающих, по крайней мере, один раз все нули.
Этап 4. Перестановка некоторых нулей. Находится наименьший элемент в невычеркнутых клетках, вычитается из каждого элемента для непомеченных столбцов и прибавляется к каждому элементу непомеченной строки. Результаты заносятся в “новую таблицу”.
Эта операция не изменяет оптимального решения. После неё выполняется новая итерация, цикл расчёта начинается с этапа 2 и так до тех пор, пока не будет получено оптимальное решение, т. е. пока не будет получена система независимых нулей (число нулей, отмеченных звёздочкой равно n).
Пример выполнения задания __.
Проиллюстрируем применение рассмотренного алгоритма Венгерского
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.