Надежность, ее развитие и функции

Литература

1.  И.Я.Меньшиков, А.И.Королев, Р.М.Ягудин “Надежность в ж.д. системах А и Т”. М., тр-т, 1976 г.

2.  И.Е.Дмитренко “Техническая диагностика и автоконтроль в ж.д. системах А и Т”. М., тр-т, 1976 г.

3.  Б.С.Соцков “Основы теории и расчета надежности элементов и устройств автоматики и вычислительной техники”. М., 1970 г.

4.  К.Капур и Л.Ланберсон “Надежность в проектировании систем”. М.:”Мир”, 1980 г.

5.  Беккер и Йенсон “Проектирование надежных элементных систем”. М., 1977 г.

I. Введение.

Первые статьи по анализу надежности энергетических систем появились в нашей стране в 30-х годах, а начало развития теории надежности в нашей стране относят к концу 50-х годов, тогда под руководством академика Гнеденко была основана советская школа, занявшая сразу передовые позиции в мире. На Западе теория надежности стала развиваться в начале 60-х годов, хотя отдельные работы появились в 40-х годах. Повышенный интерес к теории надежности был проявлен в начале 70-х годов и связано это было с многочисленными отказами сложных систем.

Проблема надежности со временем обостряется. К причинам такого положения можно отнести рост сложности современных тех.систем, интенсивность режимов работы систем в условиях низких и высоких температур, перепадов давления, значительных ускорений, вибрации, радиации, повышение требований к качеству функционирования систем, повышение ответственности функций выполняемых систем, повышение технической и экономической цены отказов, автоматизация процессов, исключающая непрерывное наблюдение и контроль за функционированием системы человеком.

2. Обеспечение надежности.

Под надежностью понимается свойство системы выполнять заданные функции, сохранять свои эксплуатационные показатели в заданных пределах при определенных режимах работы в течение требуемого промежутка времени или требуемой наработки.

Исходя из определения надежности очевидно:

1.Надежность носит вероятностный характер;

2.Возможно появление сбоев и отказов в работе системы; 

3.Необходимо оценивать соответствие с заданным режимом эксплуатации систем.

Проблема обеспечения надежности связана со всеми этапами ее создания и ее практического использования. Надежность сохраняется применением правильных способов хранения изделий и поддерживается правильной их эксплуатацией, планомерным уходом, профилактикой и ремонтом. При проектировании изделий должны учитываться следующие факторы:

1.Качество применяемых изделий и компонентов;

2.Доступность всех частей, деталей для осмотра, контроля и ремонта;

3.Режим работы компонентов и деталей;

4.Защитные устройства.

При проекировании систем автоматического управления и регулирования необходимо такое построение схем, чтобы отказ в работе одного элемнта не приводил к аварийному состоянию всей системы.

В случаях когда этого не удается добится, следует вводить специальные элементы и устройства, переводящие систему на более низкий уровень автоматизации при условии сохранения безопасности. Важную роль в обеспечении надежности систем занимает строгое соблюдение технологических процессов при изготовлении систем. При эксплуатации устройств основными факторами, влияющими на надежность являются:

1.Климатические и производственные условия эксплуатации;

2.Научно обоснованная тщательно продуманная система обслуживания, которая имеет решающее значение для сохранения заданной надежности системы;

Квалифицированное и ответственное обслуживание персонала имеет большое значение для сохранения надежности.Так, например, от общего числа отказов - 20% отказов происходит из-за ошибок, допущенных при производстве устройств;

30% - от эксплуатационных условий и неправильных режимов эксплуатации;

5-7% - за счет старения и износа устройств.

3. Основные понятия и термины теории надежности.

Система - это совокупность взаимосвязанных элементов, предназначенных для выполнения опред. задач.

Элемент (элемент системы) - составная, простейшая часть системы.

В совокупность качественных свойств, определяющих надежность функционирования объекта входят:

·  безотказность - это свойство объекта выполнять возложенные на него функции в требуемый момент времени при заданных условиях;

·  ремонтопригодность - это свойство объектов, заключающиеся в его приспособленности к предупреждению, отысканию и устранению в нем отказов и неисправностей путем проведения восстановительных работ. Под востановительными работами понимается тех. обслуживание и ремонт.

·  долговечность - это свойство объекта сохранять свою работоспособность в процессе длительной эксплуатации, хранения и транспортировки.

·  сохраняемость - это свойство объекта сохранять обусловленные эксплуатационные показатели в течение и после установленного срока хранения, определяемого техническими условиями.

Для ж.д. систем АиТ помимо указанных качественных показателей надежности вводят качественный показатель - живучесть.

Живучесть - это способность объекта сохранять свои основные функции хотя бы при понижении эффективности работы всего объекта при воздействии на него отказов.

Для правильной оценки надежности функционирования объекта необходимо четко определить понятие отказов.

Отказ - это событие, заключающееся в полной или частичной утрате работоспособности объекта.

Классификация отказов.

1. По характеру проявления бывают:

·  внезапные отказы;

·  постепенные отказы.

2. По степени влияния на работоспособность:

·  полный отказ;

частичный отказ.

3. По связи с другими отказами:

·  независимые;

·  зависимые.

4. По времени существования отказов:

·  устойчивый;

·  самоустраняющийся;

·  перемежающийся ( частое проявление сбоев одного и того же характера).

5. По наличию внешних проявлений отказов:

·  очевидные;

·  скрытые.

6. По причине появления отказов:

·  конструкционные;

·  производственные;

·  эксплуатационные.

7. По природе происхождения:

·  естественные;

·  искусственные.

8. По времени возникновения отказов:

·  при испытаниях;

·  периода приработки;

·  периода нормальной эксплуатации;

·  отказы последнего периода эксплуатации.

9. По возможности устранения отказов:

·  устраняемый отказ;

·  неустраняемый.

Дефект не приводит к потере работоспособности объекта, а только может способствовать появлению отказа. Все существующие объекты с точки зрения теории надежности обычно разделяют на 2 большие группы - невосстанавливаемые объекты и восстанавливаемые объекты.

Невосстанавливаемые объекты - это такие, работа которых после отказа считается полностью невозможной или нецелесообразной. 

Однако к невосстанавливаемым объектам можно отнести не только те, которые не могут быть принципиально отремонтированые. Само понятие невосстанавливаемый объект характеризуется не видом аппаратуры, а ее спецефическим назначением.

Под невосстанавливаемыми объетами в теории надежности понимают также объекты, отказ которых в процессе функционирования приводит к непоправимым последователям.

Под восстанавливаемым (ремонтируемым объектом) понимается такой, работа которого может быть восстановлена после проведения восстановительных работ (ремонта).

4. Количественные показатели надежно-невосстанавливаемых систем.

При рассмотрении статистических показателей надежности невосстанавливаемых систем будем рассматривать такую схему испытаний, когда несколько образцлв работают до полного отказа. В этом случае статистические показатели в пределе с ростом числа испытаний будут сходится по вероятности с аналогичными вероятностными показателями.

1. Вероятность безотказной работы объекта в интервавле времени от нуля до t₀.

а) вероятностное определение

P(t₀)=P(0,t₀)=P(Q³t₀)=1-F₁(t₀)         (1)

Q - случайное время работы объекта до отказа;

      F₁(t₀) - функция распределения случайной величины Q;

P(t₀) - вероятность того, что объект проработает безотказно в течении заданного времени t₀ при условии, что в момент времени t=0 он был исправным, или, что то же самое, — это вероятность того, что время работы объекта до отказа больше или равно заданному времени t₀.

б) статистическое определение

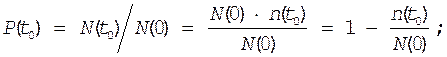      (2)

N(t₀) - количество исправных объектов к моменту времени t₀;

N(0)     - количество исправных объектов в начальный момент времени;

n(t₀) - количество отказавших объектов за время t₀; 

  Номер объекта

   1

  2

  3

  4

  5

  6

  7

  8 

t₀              t

Рис.1. Схема поясняющая статистическое определение

Чем больше проведено испытаний, тем с большей доставерностью статистическая оценка вероятности безотказной работы характеризует надежность объекта и тем ближе она к вероятностной оценке.

Вероятность безотказной работы обладает следующими свойствами

0£P(t)£1

P(o)=1

P(¥)=0

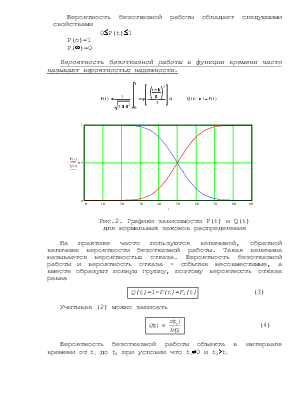
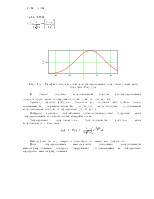
Вероятность безотказной работы в функции времени часто называют вероятностью надежности.

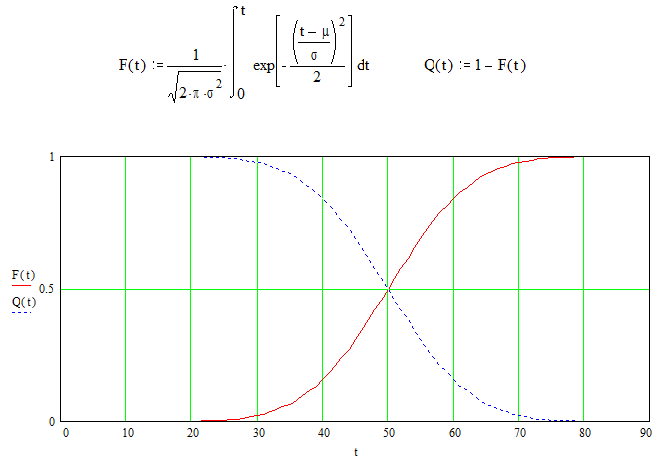
Рис.2. Графики зависимости Р(t) и Q(t)

для нормальных законов распределения

На практике часто пользуются величиной, обратной величине вероятности безотказной работы. Такая величина называется вероятностью отказа. Вероятность безотказной работы и вероятность отказа - события несовместимые, а вместе образуют полную группу, поэтому вероятность отказа равна

                 Q(t)=1-P(t)=F₁(t)              (3)

Учитывая (2) можно записать

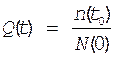                                                                                                                                             (4)

Вероятность безотказной работы объекта в интервале времени от t₁ до t₂ при условии что t₁¹0 и t₂>t₁

а) Вероятностное определение

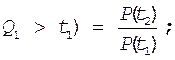при условии, что                     (5)

где: P(t₁,t₂)- условная вероятность того, что случайное время работы объекта до отказа окажется больше времени t₂ при условии, что объект уже проработал безотказно до момента времени t₁.

б) Статистическое определение

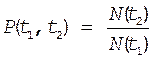                                                                                                               (6)

Вероятность безотказной работы объекта в интервале от t₁ до t₂ равна отношению числа исправно-работающих объектов к моменту времени t₂ к числу исправно-работающих объектов к моменту времени t₁.

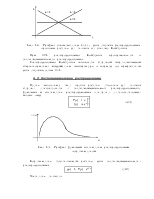
3. Частость отказов или плотность распределения отказов.

а) Статистическое определение

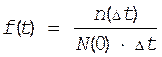                                                                                                                                (7)

Частость отказов равна отношению числа отказавших объектов в интервале времени Dt к произведению числа исправных объектов в начальный момент времени на ширину интервала.

? ? ? ? ? ? ? ?

б) Вероятностное определение

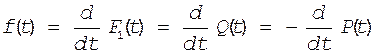                                                                             (7^*)

Пример: Производится испытание диодов на надежность по параметру обратное пробивное напряжение. Испытываемая партия 1000 шт. Требуется определить частость отказов в интервале времени =100 часов. При этом известно, что в течении первых 5 тыс. часов отказало 100 диодов, а в интервале от 5тыс. - 5 тыс.100 часов отказало еще 50 диодов.

Р е ш е н и е.

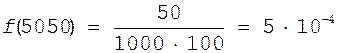
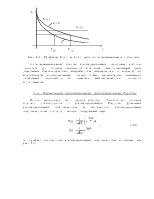
4. Интенсивность отказов в момент времени t.

а) Статистическое определение

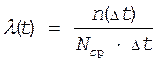                                                                                                                (8)

Интенсивность отказа равна отношению числа отказавших объектов за интервал времени Dt к произведению среднего числа исправных объектов в интервале Dt на длительность этого интервала.

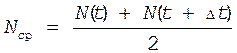  б) Вероятностное определение

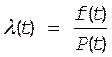
Для предыдущего примера определим интенсивность отказа

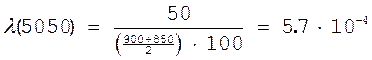
Таким образом из рассмотрения 2-х последних показателей следует, что частость отказов представляют собой скорость изменения условий вероятности отказа при условии, что в начальный момент времени объект неисправен, а интенсивность отказа представляет собой скорость изменения условной вероятности отказа при условии, что на момент времени t объект неисправен.

5. Среднее время работы объекта до отказа.

Это время является математическим ожиданием времени безотказной работы. Приблизительно среднее время безотказной работы однотипных элементов партии определяется

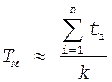                                                                                                                                 (9)

где: t_i - время исправной работы i-ого элемента в партии;

k - количество элементов в партии.

На практике чаще пользуются следующим выражением

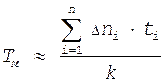                                                                                               (10)

n

Число отказавших обектов .

                           tn

полное время  

Рис.3. Пояснение к формуле (10)

Dn_i - кол-во отказавших объектов в i-ом интервале;

t_срi - среднее значение времени в i-ом интервале.

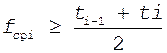
5. Зависимости между вероятностными показателями

надежности.

5(I). Связь между f(t), P(t) и или Q(t).

Согласно формуле (7) статистическое определение f(t) равно

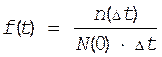
Рассмотрим f(t)  как непрерывную функцию, для этого устремим интервал Dt®0, тогда можно записать

                                                                                      *

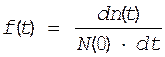Продифференцируем ф-лу (2) статистического определения вероятности безотказной работы

                                                              **

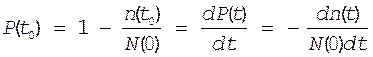Сравним между собой выражения (*) и (**), тогда имеем

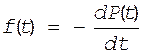                                                              ,                                                      (11)

а учитывая что P(t)=1-Q(t) получим

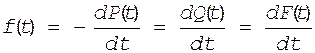                                                                       (12)

Проверка Q(t)=F(t), где F(t)- функция распределения времени безотказной работы или интегральный закон распределения времени безотказной работы.

Если проинтегрировать уравнение (12) в интересующих нас пределах, то можно получить значение вероятности отказа

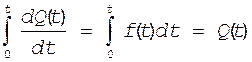                                                                      (13)

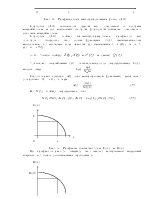
Тогда вероятность безотказной работы будет равна

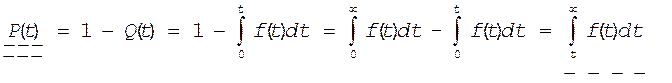
или

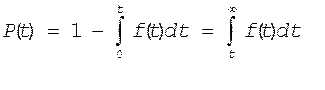                                                                                    (14)

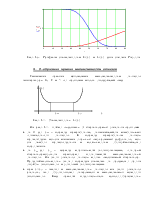
Q(t)      P(t)

0               t                                t  

Рис.4. Графическая интерпретация ф-лы (14)

Формула (14) является одной из основных в теории надежности и ее называют второй формулой записи основного закона надежности.

Формула (14) можно проиллюстрировать графиком из которого следует, что если функция f(t) аналитически известна, то площадь под кривой до значения , а от t до .

5.2. Связь между  и P(t) и (или) Q(t)

Согласно выражению (8) статистическое определение l(t) имеет вид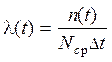                                                          

Рассмотрим теперь  как непрерывную функцию, для чего устремим , тогда

                                                                                              (*)

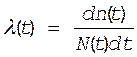Но N(t) можно определить как

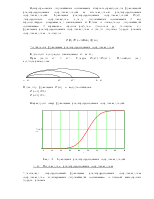
         N(t)=N(0)-N(0)·Q(t)=N(0)·(1-Q(t))=N(0)·P(t)       (**)

P(t)                      

1

                    t    

0           t     

Рис.5. Графики зависимости P(t) и N(t)

Из графиков рис.5. видно, что число исправных изделий падает по мере увеличения времени t

N(t)

 N(0)

                    t    

0           t     

Подставим значение (**) в (*) получим

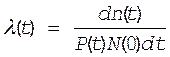                                                                             (15)

Но очертанная часть выражения (15) - это есть не что иное, как f(t), тогда имеем

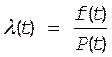                                                                                                                                              (16)         или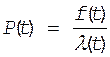                 

Из (16) следует что  , т.к. P(t)£ 1

Формула (16) может встречаться и в таких записях

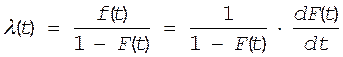
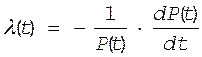
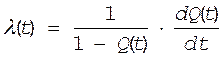
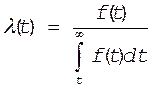
5.3. Связь между  и P(t)

Из п.5(2). следует. В п. 5.3. показано, что

           (**)

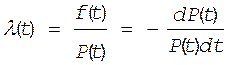Проинтегрируем левую и правую часть выражения (**) в пределах от 0 до t

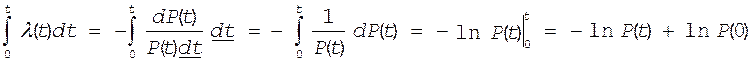
введем обозначение x=P(t), тогда 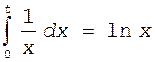, но P(0)=1, а ln1 = 0, (e⁰=1), тогда

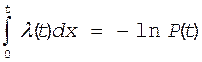       или

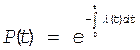                                       (17)    

Напомним, вторая форма записи имеет вид

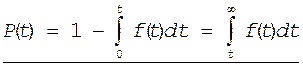
Предположим, что , тогда из (17) следует

                                           (18)

5.4. Связь между T и P(t).

Среднее время работы объекта до отказа или наработка на отказ является не чем инным, как математическим ожиданием случайного времени безотказной работы объекта Q.

Тогда для непрерывной величины времени t при известном законе плотности распределения f(t) имеем

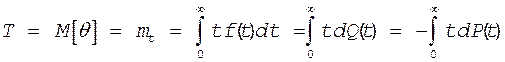                                                   (19)

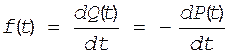
Выражение (19) проинтегрируем по частям. Для этого произведем замену переменных t=u,  du=dt, P(t)=V, dP(t)=dV

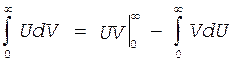
Тогда имеем

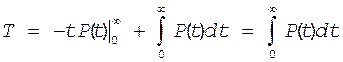
           P(¥)=0   0

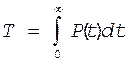                                            (20)

Подставим в (20) значение P(t) из 18 при условии что  ,  тогда

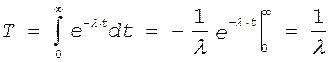
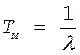                                                                                                             (21)

5.5. Взаимосвязь между основными показателями.

Таблица 1

6. Определение показателей надежности по эмпирическим данным.

Существуют два пути определения показателей надежности:

·  теоретический;

·  экспериментальный.

Теоретический способ основан на вероятностном представлении показателей надежности.

Экспериментальный - на статистич. представлении показателей надежности.

6.I. Определение показателей надежности для случая репрезентативной (представительной) выработки большого объема.

Репрезентативная выработка - это токая выработка из генеральной совокупности, параметры которой с достаточной достоверностью характеризуют саму генеральную совокупность.

Определение показателей надежности рассмотрим на следующем примере.

Пример.  Проводились испытания на надежность 64 стабилизированных источников питания устройств АТС. При этом событие “отказ” регистрировалось как при пропадании напряжения источника, как и при выходе напряжения за допустимые пределы. Испытания проводились до отказа всех источников испытываемой партии. При этом время выхода из строя каждого источника исчислялось от момента начала испытания. Результаты испытаний представлены в табл.2.

Определение вероятности безотказной работы производят по формуле (2)

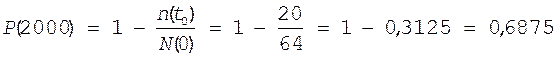
Таблица 2

Результаты испытаний источников питания.

Оценку интенсивности отказов определим по формуле (8).

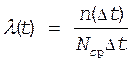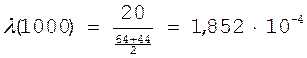;                           1/час

Оценку среднего времени наработки до отказа определим по формуле (10).

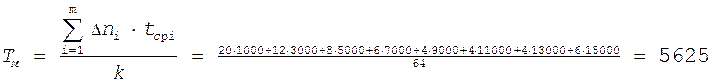  часов

Результаты расчетов удобно представлять в виде табл.3.

Таблица 3

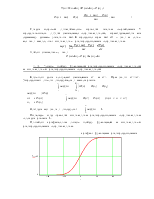
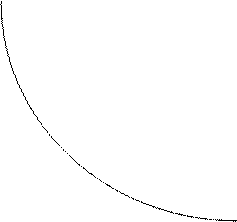
По полученным данным начертим графики функций надежности и зависимости интенсивности отказов от времени.

  P

  1,0

 0,8

  0,6

  0,4

  0,2

0    2 4 6 8 10 121416   t×10³

Рис.6. Графики зависимости P(t) и l(t)

6.2. Определение показателей надежности для случая выработки малого объема.

В математической статистике разработаны методы, которые позволяют по выборке малого объема составить определенное представление по всей генеральной совокупности.

Пример:Производятся испытания на надежность 8 систем связи.

В табл.4. представлены результаты испытаний.

Таблица 4

Для определения вероятности безотказной работы и интенсивности отказов используем имперические формулы, выведенные из опыта математической статистики для случая малых выборок.

Оценка вероятности безотказной работы для случая малых выборок равна

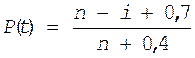                                                                                                                          (22)

где: n - объем выборки

i - номер появления отказа

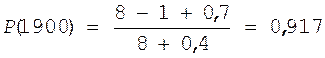
Оценка интенсивности отказов производится по формуле

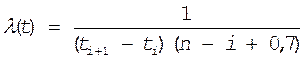                                                                                                  (23)

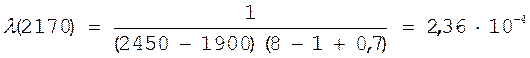   1/час

Оценка среднего времени наработки на отказ определим по формуле - (9)

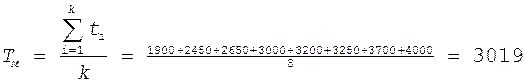    час

Результаты расчетов сведены в табл.5.

Таблица 5

l×10-4   8   6   4   2      0

   P

 1,0

0,5

0 500 1000  2000      t

Рис.7. Графики зависимости P(t) и l(t)

7. Понятие о распределении случайных величин.

Случайная величина - это такая величина, которая в зависимости от случая принимает те или иные значения с определенными вероятностями.

Если существует вероятность того, что величина Х£х для всех действительных чисел х, то величина Х будет случайной