12. РАСЧЁТ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ
12.1. Оценка передачи
Наибольшее распространение в машиностроении получила простая планетарная передача (редуктор Джеймса, рис. 10, а, б), где ведущее звено — солнечное колесо 1, ведомое – водило h, в котором закреплены оси сателлитов 2. Корончатое колесо 3 встроено в неподвижный корпус редуктора.
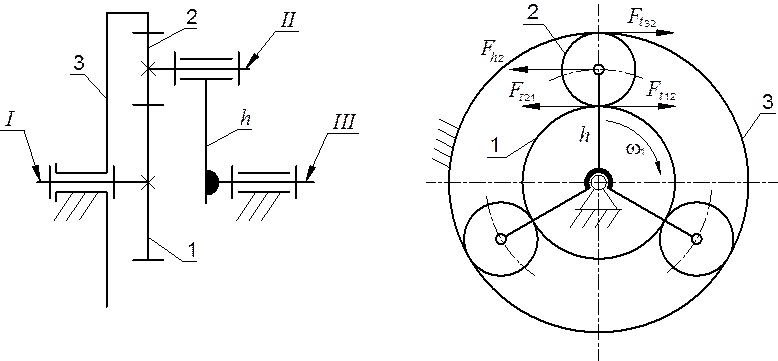 а) б)
а) б)
Рис. 10. Простая планетарная передача
По сравнению с обычной зубчатой передачей она имеет преимущества.
1. Широкие кинематические возможности, позволяющие использовать передачу либо как редуктор с постоянным передаточным отношением, либо как коробку скоростей, либо как дифференциальный механизм.
2.
Компактность и малая масса передачи (приблизительно в два раза),
объясняемые: а) передачей мощности по нескольким потокам (по числу сателлитов),
б) наличием внутреннего зацепления, обладающего повышенной нагрузочной
способностью, в) значительным передаточным отношением (![]() =
3...8).
=
3...8).
3. Малая нагрузка на опоры вследствие взаимного уравновешивания сил, действующих на сателлиты.
4. Более высокий КПД.
Недостатки:
1. Сложность конструкции.
2. Неравномерность распределения нагрузки между сателлитами.
12.2. Расчёт чисел зубьев
В отличие от обычных зубчатых передач расчёт планетарных передач начинают с выбора чисел зубьев колёс. При назначении чисел зубьев необходимо учитывать ряд ограничений:
а) числа зубьев должны быть целыми числами;
б) выбранные числа зубьев должны давать передаточное отношение i с допустимой точностью Di; по ГОСТ 2185 при i ³ 3,5 Di = ± 4 %;
в) рекомендуется для большинства случаев использовать нулевые прямозубые колёса с ограничениями числа зубьев для колёс с наружными зубьями из условия неподрезания — zн. min = 17, для колес с внутренними зубьями из условия правильного зацепления (отсутствия интерференции) — zв. min = 19; со смещением колёса проектируют при z < 17 или при вписывании в стандартное межосевое расстояние.
В планетарной передаче есть и другие ограничения, так как колёса взаимосвязаны. Основная цель выбора чисел зубьев — обеспечение заданного передаточного отношения
![]() , (48)
, (48)
откуда
![]() . (49)
. (49)
Задаваясь числом зубьев солнечного колеса z ³ 17, определяют число зубьев корончатого колеса z3. Число зубьев сателлитов определяют из условия соосности
![]() . (50)
. (50)
Невыполнение условия соосности (если z2 — не целое число) и нижеследующих условий требует увеличения z1 и пересчёта z3 и z2.
Условие сборки проверяют по зависимости
![]() , (51)
, (51)
где пс – число сателлитов, обычно принимают пс = 3; g – любое целое число.
Условие соседства
![]() (52)
(52)
гарантирует отсутствие интерференции соседних сателлитов. На интерференцию также проверяется внутреннее зацепление (условие правильности внутреннего зацепления). По этому условию числа зубьев сателлитов 2 и корончатого колеса 3 должны соответствовать табл. 13.
Таблица 13
|
Число зубьев сателлитов z2 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
Число зубьев колеса z3 |
>144 |
>81 |
>60 |
>50 |
>44 |
>41 |
>38 |
>36 |
>35 |
Подбор чисел зубьев с оптимизацией по габаритам может быть выполнен также по методу пропорций и на ЭВМ (программа ТМ22, алгоритм расчёта изложен в пособиях [4, 5]).
Пример 7. Рассчитать
числа зубьев планетарной передачи по схеме рис. 10 по следующим исходным
данным: передаточное отношение ![]() = 6,5; число сателлитов
пс = 3.
= 6,5; число сателлитов
пс = 3.
Решение.
1) В папке ТММ выводим курсор на gwbasic.exe (вход в систему BASIC) и нажимаем клавишу ENTER.
2) Нажимаем функциональную клавишу F3 (на дисплее высветится «LOAD» – загрузка) и набираем ТM21 ENTER.
3) Нажимаем функциональную клавишу F2 (на дисплее высветится «RUN» – запуск) и набираем ENTER. Клавишу ENTER в дальнейшем нажимаем после каждого ввода.
4) Вводим исходные данные.
1 – шифр редуктора Джеймса.
7 – передаточное отношение.
.04 – допускаемое отклонение передаточного отношения (4%).
3 – число сателлитов.
.96 – КПД одной зубчатой ступени (0,95…0,97).
17 – минимальное число зубьев.
150 – максимальное число зубьев.
Распечатка компьютерных данных приведена на рис. 11.
*********************** РЕДУКТОР ДЖЕЙМСА ***********************
** Числа зубьев **
** солнечного колеса 17
** сателлитов 37
** корончатого колеса 91
** Передаточное отношение 6.35
** Отклонение передаточного отношения -0.0226
** КПД редуктора 0.934
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.