Ориентировочный расчёт валов. Эскизная компоновка редуктора. Приближённый расчёт валов редуктора, страница 5

1.  Вычерчивают оси солнечного колеса и сателлита, располагая их на межосевом расстоянии a_w.

2.  Вычерчивают контуры сателлита и b ´ d_a, располагая его на оси. Длина оси сателлита складывается из ширины сателлита b, двух пар зазоров D₁ и D₂ и двух толщин щёк d₂.

3.  Диаметр оси dопределяют из расчёта по изгибающему моменту

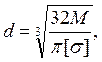                                                       (189)

где М - изгибающий момент, Н·м; М = ·L/4;  - сила, действующая на сателлиты, Н (см. п. 12.4); L – расстояние между опорами водила, мм; L= b+ 2·(D₁ + D₂ ) + d₂; d₂ – толщина щёк, мм; d₂ = 2d; [σ] – допускаемое изгибное напряжение, МПа; [σ] = 0,3· σ_т.

Диаметр оси округляют по стандартам для подшипников.

4.  В зависимости от ширины сателлита b назначают один или два подшипника сателлита. Наружный диаметр D принимают из возможности проектирования обода сателлита толщиной d_о = 3m. Этому условию соответствует диаметр D= m(z- 7).

5.  Вычерчивают валы  с диаметрами и конструктивными решениями, принятыми в ориентировочном расчёте.

6.  Для выравнивания  нагрузки между сателлитами проектируют плавающее солнечное колесо с зубчатой муфтой. На быстроходном валу и на колесе нарезают венцы муфты, которые входят во внутреннее зацепление с корпусом муфты. Делительный диаметр венцов муфты принимают d_м = 1,5d_бх, корректируя его в соответствии с формулой d_м = m_мz_м; наружный диаметр муфты D_м = d_м + 7m_м. Ширина венцов муфты b_м = (0,2…0,3) d_м, длина муфты l_м = (0,8…1) d_м. Модуль зубьев муфты может быть равен модулю колёс: m_м = m.

7.  Назначают зазор  между наружным диаметром муфты D_м и внутренним диаметром пустотелого вала водила D₇ = m_м (d_вд.в =  D_м  + 2D₇), наружный диаметр вала водила (под подшипником) принимают  d_вд.н = 1,25 d_вд.в и округляют по стандартам для подшипников.

8.   Конструктивно принимают  радиальные подшипники водила лёгкой серии с зазорами до торца оси водила D₁; измеряют расстояние L_h между серединами подшипников.

9.   Назначают радиальные  подшипники быстроходного вала солнечного колеса с зазором до муфты D₁ и расстоянием между их серединами L₁ = d_бх.

10.  Длину  консолей назначают по рекомендациям (183) и (184).

19. ПРИБЛИЖЁННЫЙ РАСЧЁТ ВАЛОВ РЕДУКТОРА

Данная методика даёт более достоверные результаты, чем ориентировочный расчёт, так как диаметр вала определяют из расчёта на сложное напряженное состояние при действии крутящего и изгибающего моментов. В данном разделе исходными данными расчёта являются: силы, действующие на колёса, шкивы, звёздочки и т.д., расстояния между линиями действия всех сил, диаметры колёс.

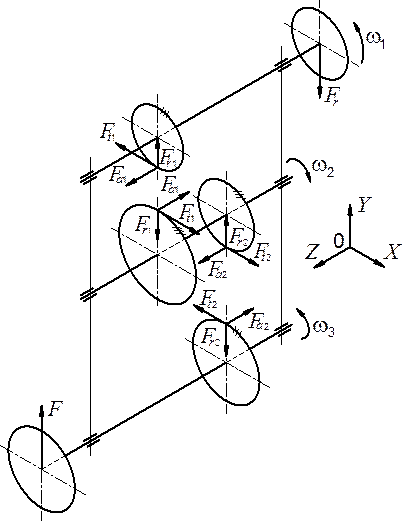Рис. 36. Аксонометрическая проекция колёс редуктора

Неправильное приложение действующих нагрузок — типичная ошибка при разработке расчётной схемы. Весьма полезна аксонометрическая схема нагружения валов. На рис. 36 представлена схема двухступенчатого цилиндрического редуктора, на быстроходном валу которого расположен шкив ремённой передачи. На шкив действует нагрузка  F_r от натяжения ремней. Тихоходный вал редуктора нагружен силой Fот цепной передачи. При составлении схем необходимо помнить правила.

1.  На колёса и другие детали действуют сосредоточенные нагрузки, которые заменяют сосредоточенными  силами и прикладывают посередине их ширины.

2.  Точку приложения сил находят по кинематической схеме привода и схеме нагружения валов. Обратить внимание на точки приложения сил в червячно-цилиндрическом редукторе.

3.  На шестерню и колесо действуют силы, равные по модулю, но противоположно направленные.

4.  Радиальные силы F_r в зацеплении всегда направлены от точки контакта по радиусу к оси вала.

5.  Окружные силы F_t  создают вращающие (крутящие) моменты и направлены: на шестерне — против направления вращения, на колесе — по направлению вращения.

6.  Осевые силы F_a1 и F_a2на промежуточном валу направляют в противоположные стороны с целью снижения осевой нагрузки на подшипники. В этом случае шестерня и колесо будут иметь одинаковые направления зубьев (оба левые или правые) в редукторах, выполненных по развёрнутой схеме (рис. 30). В соосных редукторах (рис. 31) они имеют разные направления.