![]() = 0,005 рад (0,3°) – для шарикоподшипников радиальных;
= 0,005 рад (0,3°) – для шарикоподшипников радиальных;
![]() = 0,0025 рад (0,15°) – для роликоподшипников радиальных;
= 0,0025 рад (0,15°) – для роликоподшипников радиальных;
![]() = 0,05 рад (2…3°) – для шарикоподшипников сферических;
= 0,05 рад (2…3°) – для шарикоподшипников сферических;
![]() = 0,001 рад (0,06°) – для подшипников скольжения.
= 0,001 рад (0,06°) – для подшипников скольжения.
Б) Крутильная жесткость.
При расчёте валов на деформацию кручения определяют угол закручивания j. При недостаточной крутильной жёсткости в конструкции вал-шестерня изменяется угол наклона b, что приводит к концентрации нагрузки. В делительных и отсчётных механизмах упругие перемещения снижают точность измерений и т.д. Перемещение при кручении валов постоянного диаметра определяют по формуле:
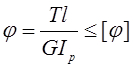 , (23.14)
, (23.14)
где G – модуль сдвига; для сталей G = 0,8·105 МПа.
Значения допускаемых углов закручивания валов колеблется в широких пределах в зависимости от требований, предъявляемых к механизму. Например, в приводах следящих систем, делительных механизмах и т.д. допускаемые углы ограничивают секундами и минутами на 1 м длины, а в карданных валах автомобилей допускают несколько градусов на метр. Для трансмиссионных валов механизма передвижения мостовых кранов рекомендуется [j] = (4…6)×10-3 рад/м = (0,25…0,35 град/м).
Малое значение допускаемых перемещений иногда приводит к тому, что размеры вала определяет не прочность, а жёсткость. В этих случаях нецелесообразно изготовлять вал из дорогих высокопрочных сталей. Так, анализ формул (23.12)…(23.14) показывает, что величины упругих перемещений (d, θ, j) уменьшаются с увеличением диаметров и моментов инерции I, Ip, которые растут с уменьшением прочности материала.
Пример 23.4. Выполнить проверку на крутильную жёсткость вала: крутящий момент на валу: Т1 = 161,9 Н·м, диаметр хвостовика dх = 25 мм, [j] = 0,25 град/м.
Решение.
Назначаем длину
хвостовика lх = 1,5dх = 1,5·25 = 37,5 мм. Принимаем lх = 40 мм. Назначаем длину скручивания
0,5lх = 0,5·40 = 20 мм. Полярный момент
инерции Iр = π![]() /32 = π·254/32 = 9287 мм4. Угол
закручивания – формула (23.14):
/32 = π·254/32 = 9287 мм4. Угол
закручивания – формула (23.14):
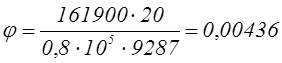 рад = 0,25 град = [0,25].
рад = 0,25 град = [0,25].
Вывод. Крутильная жёсткость достаточна.
23.8. Расчёт на виброустойчивость
Колебания валов с расположенными на них деталями и узлами возникают при действии внешних постоянно действующих и периодически изменяющихся сил и связаны с упругой деформацией валов. Малые колебания около положения равновесия становятся опасными для вала и конструкции в целом, когда частота возмущающей силы достигает частоты собственных колебаний системы, то есть когда наступает резонанс. При этом напряжения в сечениях вала существенно возрастают и определяются, в основном, не внешней нагрузкой, а силами инерции колеблющихся масс.
Резонанс представляет собой большую опасность для прочности конструкций и его следует избегать. Наиболее часто его предотвращают за счёт изменения частоты собственных колебаний, реже – за счёт изменения частоты возмущающей силы.
Одна из основных задач расчета конструкции на колебания (на виброустойчивость) состоит в определении частот собственных колебаний и установлении допустимой угловой скорости, ограничиваемой частотой собственных колебаний. Изгибные колебания валов связаны с их изгибной деформацией. На рис. 23.8 приведена схема вала с закреплённым на нём зубчатым колесом, который рассматривают как балку с сосредоточенной массой, шарнирно закрепленную в жёстких опорах.
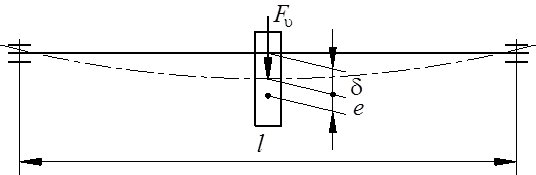 |
Рис. 23.8. К расчёту на виброустойчивость
Вращающиеся детали не могут быть идеально сбалансированы из-за неизбежных погрешностей технологического характера. Поэтому на практике всегда возникают инерционные силы от дебаланса е, которые уводят вращающиеся на валу детали от оси вращения. При определенной угловой скорости дебаланс вызывает сильную «раскачку» системы. Угловую скорость, при которой наступает равенство центробежных сил и сил упругости, называют критической. Центробежная сила:
![]() (23.15)
(23.15)
Величина прогиба при действии силы Fu:
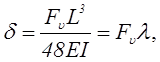 откуда
откуда 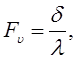 (23.16)
(23.16)
где λ – податливость в мм/Н, то есть деформация, вызываемая единичной силой:
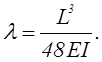 (23.17)
(23.17)
Приравнивая правые части уравнений (23.15) и (23.16), получают:
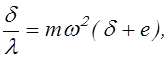 откуда
откуда
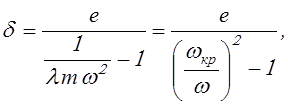 (23.18)
(23.18)
В формуле (23.18) принято
обозначение ![]() Критическая угловая скорость
Критическая угловая скорость
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.