
















6 ФІЗИКА АТОМІВ І МОЛЕКУЛ. ОСНОВИ КВАНТОВОЇ
МЕХАНІКИ. ФІЗИКА ТВЕРДОГО ТІЛА. ЯДЕРНА ФІЗИКА
ТА ЕЛЕМЕНТАРНІ ЧАСТИНКИ
Основні формули
Теорія Бора
Квантування моменту імпульсу електрона (перший постулат Бора)
Ln = n![]() або mV nr n = n
або mV nr n = n![]() ,
,
де m - маса електрона; Vn - швидкість електрона на n - й орбіті; rn - радіус; n- ї
стаціонарної орбіти; ![]() - стала Планка.
- стала Планка.
Радіус n – і стаціонарної орбіти
rn = aon2 ,
де ао - перший боровський радіус.
Дозволені значення енергії електрона для воднеподібних атомів
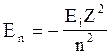 ,
,
де Еі - енергія іонізації атома; Z - порядковий номер атома.
Енергія кванта, випромінена чи поглинута атомом при переході електрона з одного стаціонарного стану у другий,
Еn - Em = hn,
де n - частота фотона
Узагальнена формула Бальмера
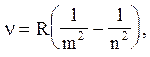
де R - стала Рідберга ( R = 3,29 . 1015с-1)
Хвильові властивості частинок.
Співвідношення де Бройля l=R/h,
де l - довжина хвилі де Бройля; Р - імпульс частинки.
Зв’язок між довжиною хвилі та частотою
ln = с; w = 2pn,
де с - швидкість світла у вакумі.
Імпульс частинки та його зв’язок з кінетичною енергією Ек
а) Р = moV; Р2 = 2mEк,
б)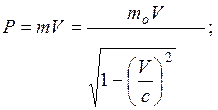
![]() ,
,
де mo - маса спокою частинки;
m - релятивістська маса;
V - швидкість частинки;
Ео - енергія спокою частинки.
Співвідношення невизначеностей
а) Dх . Dрх
³ ![]() , ( для координати
та імпульсу),
, ( для координати
та імпульсу),
де Dрх - невизначеність проекції імпульсу на вісь Х; DC - невизначеність координати;
б) DE . Dt ![]() ( для
енергії та часу),
( для
енергії та часу),
де DE - невизначеність енергії; Dt - час життя квантової системи у даному енергетичному стані.
Одномірне рівняння Шредінгера для стаціонарних станів
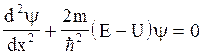 ,
,
де y(х) - хвильова функція, яка описує стан частинки; m - маса частинки; Е - повна енергія; U - потенціальна енергія частинки.
Густина імовірності
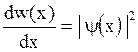 ,
,
де dw(x) - імовірність того, що частинка може бути виявлена біля точки з координатою х на відрізку dх.
Рішення рівняння Шредінгера для одномірної глибокої прямокутної «потенціальної ями»
а) 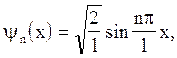 (власна
хвильова функція)
(власна
хвильова функція)
б) Еn = ![]() (власні значення енергії)
(власні значення енергії)
де n - квантове число ( n = 1, 2, 3, ...);
![]() - ширина ями
- ширина ями
в області l £ х £ 0 , U = ¥ і y(х) = 0
Молярний об’єм кристала
![]() =
=![]() ,
,
де М - молярна маса; r - густина кристала .
Об’єм елементарної комірки для решітки кубічної сингонії
Veл = а3,
де а – параметр решітки.
Відстань між найближчими сусідами
а) d = a (проста кубічна)
б) d = a ![]() ( об’ємноцентрована кубічна)
( об’ємноцентрована кубічна)
в) d = а/![]() ( гранецентрована
кубічна)
( гранецентрована
кубічна)
Число найближчих сусідів
а) z = 6 ( проста кубічна)
б) z = 8 ( об’ємноцентрована кубічна)
в) z = 12 (гранецентрована кубічна)
Число атомів, які приходяться на одну комірку
а) n = 1 (проста кубічна)
б) n = 2 ( О.Ц.К.)
в) n = 4 ( Г.Ц.К.)
Параметр кубічної решітки з однакових атомів
а =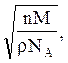
де NА - число Авогадро
Теплоємність твердих тіл.
Середня енергія квантового одномірного осцилятора
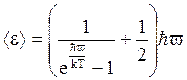
Теплоємність одиниці об’єму речовини
с = 9nk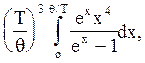
де n - число атомів в одиниці об’єму;
Т - абсолютна температура; q - температура Дебая;
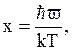 де
k -
стала Больцмана
де
k -
стала Больцмана
Елементи квантової статистики.
Розподіл вільних електронів в металі по енергіям при Т = О К
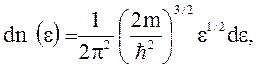
де dn(e) - концентрація електронів, енергія яких знаходиться в межах від e до
e + d e ; m - маса електрона.
eF(0) 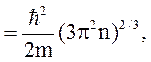
де n - концентрація електронів в металі.
Середня енергія вільних електронів при Т = О К
<E>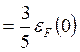
Напівпровідники.
g =en (bn + bp),
де е - заряд електрона; n - концентрація носіїв заряду ( електронів і «дірок»); bn i bp - рухливість електронів і «дірок».
Температурна залежність електропровідності напівпровідників
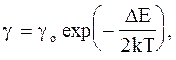
де gо - постійна величина; DE - ширина забороненої зони.
Сила струму в р - n - переході
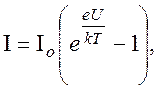
де Іо - граничне значення сили зворотного струму; U - зовнішня напруга прикладена до р - n - переходу.
Напруга при ефекті Хола
Ux = RxBJl,
де Rx - стала Хола; В - магнітна індукція; J - густина струму; l - ширина пластин.
![]() =
= 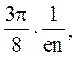
де n - концентрація носіїв заряду
Зв’язок між сталою Хола і питомою провідністю напівпровідника
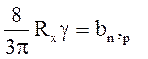 ,
,
де bn,р - рухливість електронів або «дірок»; g - питома провідність.
Атомне ядро. Радіоактивність.
Енергія зв’язку нуклонів у ядрі
Езв = {[Zmp + (A - Z)mn] - mя}c2.
Дефект маси
Dm =[Zmp + (A - Z) mn] - mя.
Закон радіоактивного розпаду
N(t) = Noexp(-lt),
де N(t) - число ядер, що не розпались до моменту часу t; No - число ядер у початковий момент часу ( t = 0 ); l - стала радіоактивного розпаду.
Середній час життя радіоактивного ядра
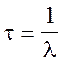
Період піврозпаду
Т1/2 = 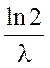
Приклади розв’язування задач
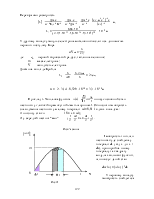
Приклад 1. Атом водню, який знаходиться в основному стані, поглинув порцію енергії 12,75 еВ і перейшов у збуджений стан. Знайти частоту обертання електрона у збудженому стані.
Розв’язання
По визначенню частота - це число обертів у одиницю
часу 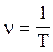 , де Т - період обертання, який
визначається швидкістю та радіусом орбіти електрона. У свою чергу ці величини
залежать від головного квантового числа n, яке
необхідно визначити.
, де Т - період обертання, який
визначається швидкістю та радіусом орбіти електрона. У свою чергу ці величини
залежать від головного квантового числа n, яке
необхідно визначити.
Атом водню може поглинути енергію тільки порціями (ІІ постулат Бора):
DE = E 1-En,
де n = 2, 3, 4 ... Для визначення n запишемо формулу квантування енергії
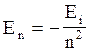 , де Еі = 13,6 еВ -
енергія іонізації атома водню.
, де Еі = 13,6 еВ -
енергія іонізації атома водню.
Звідси

Так, електрон переходить на четверту стаціонарну орбіту.
Швидкість електрона на даній орбіті можна знайти за допомогою першого постулату Бора, якщо врахуємо вираз для радіуса n -ої стаціонарної орбіти
mVnrn = n![]() (1)
(1)
rn = aon2 (2)
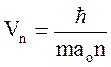 (3)
(3)
Звідси частота обертання електрона з врахуванням (2) та (3)
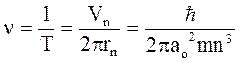
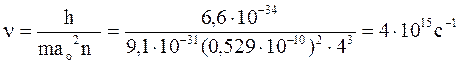
Приклад 2. Для атома водню знайти мінімальну і максимальну довжину хвилі видимої частини спектру.
Розв’язання
Видима частина спектру відповідає серії Бальмера. В узагальненій формулі Бальмера
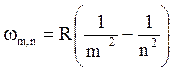 (1)
(1)
необхідно визначити
m = 2; n =3, 4, 5 ...¥
Виразимо довжину хвилі через частоту
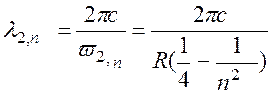 (2)
(2)
Довжина хвилі буде мати максимальне значення, коли у (2) n = 3, та мінімальне, коли n = ¥
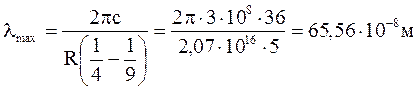 або lmax = 655,6
нм ( червоний колір)
або lmax = 655,6
нм ( червоний колір)
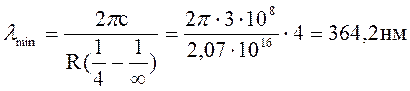 ( фіолетовий
колір)
( фіолетовий
колір)
Відповідь:
lmax = 655,6 нм; lmin= 364,2 нм.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.