Фізика атомів і молекул. Основи квантової механіки. Фізика твердого тіла. Ядерна фізика та елементарні частинки, страница 2

          Приклад 3. Порівняти дебройлівські довжини хвиль електрона, який пройшов у електронно-променевій трубці різницю потенціалів 15 кВ, і електрона, що знаходиться у атомі водню у основному стані.

                                                  Розв’язання

          Довжина хвилі де Бройля визначається співвідношенням

pl = h                                (1)

Імпульс електрона у першому випадку можливо визначити за допомогою закону збереження енергії ( енергія електричного поля  еDj переходить в кінетичну енергію електрона  p²/2m), якщо її виразити через його імпульс.

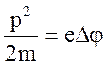                            (2)

Разом рішаємо (1) та (2), знаходимо

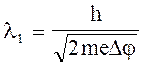                       (3)

Перевіряємо розмірність

 =

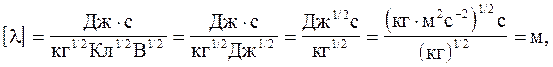
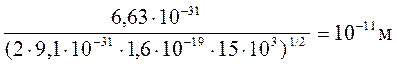
У другому випадку імпульс електрона можливо обчислити за допомогою першого постулату Бора

тVа_o =                                  

де         а_о  -  перший боровський радіус, таблична величина;

          m   -   маса електрона;

          V   -   швидкість електрона

Довжина хвилі де Бройля

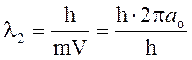 = 2pа_о,

l₂ =  2 . 3,14 . 0,529 . 10^-10 = 3,3 . 10^-10 м

          Приклад 4. Хвильова функція 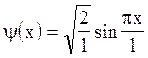  описує основний стан частинки у глибокій прямокутній «ямі» шириною l. Обчислити імовірність знаходження частинки у малому інтервалі  Dl =0,01 l в двох  випадках:

1)  поблизу стінки                       ( 0 £ х £ Dl);

2)  у середній частині “ями”          ( .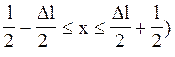

                                                  Розв’язання

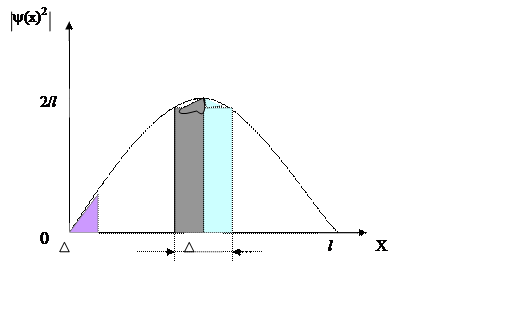
          Імовірність того, що частинка буде знайдена у інтервалі dх ( від х  до  х + dх), пропорційна цьому інтервалу та квадрату модуля хвильової функції, що описує даний стан

dw (x) =| y(x) | ²dx

	l
			l

 

Рис 41

У першому випадку імовірність знайдеться

інтегруванням  у межах від 0 до 0,011 (див. рис. 4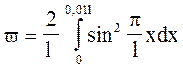1).

          (1)

знак по модулю не ставиться, бо  y - функція у даному випадку не є комплексною. Тому що  х  змінюється в інтервалі 0 £  х  £ 0,01 l , а також

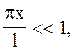 справедливо приблизне рівняння sin² 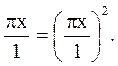                                                                                               З врахуванням цього вираз (1) набуде такого вигляду       

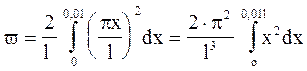                                   (2)

Псля інтегрування будемо мати

w =  2/3 p² . 10^-6 =  6,6 . 10^-6

 

               2)  Для другого випадку отримаємо

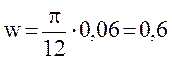
          Приклад 5. Відстань  d між сусідніми атомами кристалу  кальцію (решітка кубічна гранецентрована) рівняється 0,393 нм. Обчислити:

1)  параметр  а решітки;

2)  густину  r кристалу.

                                                            Розв’язання

1.Параметр  а решітки та відстань  d  між найближчими сусідніми атомами зв’язані простим геометричним співвідношенням (див. рис. 42)

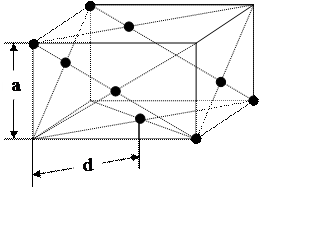                 а = d.

   Зробимо обчислення а = 0,393  нм = = 0,556 нм = 5,56 . 10^-10м

1.    Густина  r кристалу зв’язана з молярною масою М та молярним об’ємом  V_m  співвідношенням 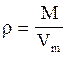                  (1)

РИС 43

                                                              

Молярний об’єм V_m знайдемо по співвідношенню

V_m = a³Z_m,                     (2)

де         a³ - об’єм одної елементарної комірки;

          Z_m - число елементарних комірок, які знаходяться у одному молі кристалу. Враховуючи, що число елементарних комірок для кристалу, який складається з однакових атомів, можливо знайти, поділивши сталу Авогадро  N_A на число атомів, які знаходяться в одній елементарній комірок, рівняння (2) можливо записати так  V_m = a³

Підставимо у (1) співвідношення   для V_m із (3),  маємо

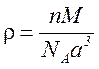
Зробимо обчислення, враховуючи, що число  n у випадку кубічної гранецентрованої решітки дорівнюється 4,

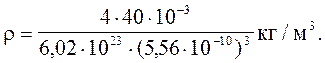=1,55 . 10³ кг/м³

Приклад 6. Обчислити теплоту DQ, яка необхідна для нагрівання кристалу  NaCl масою m = 20 г від температури Т₁ = 2 К до температури Т₂ = 4 К. Характеристичну температуру Дебая   для NаCl прийняти рівною 320 К. Умову Т<< _Д  вважати виконаною.

                                                         Розв’язання

Теплота  DQ, яка підводиться для нагрівання тіла від температури Т₁ до Т₂ , може бути обчислена по формулі

DQ 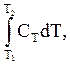 =                   (1)

де      С_Т - теплоємність тіла.

Теплоємність тіла зв’язана з молярною теплоємністю співвідношенням

С_Т = 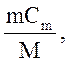                   (2)

де      m - маса тіла;

          М - молярна маса.

          Підставимо співвідношення (2) у формулу (1), маємо

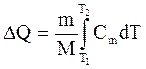                               (3)

У загальному випадку теплоємність С_m є складна функція температури, тому виносити її за знак інтегралу не можна. Однак, коли виконана умова Т<<_д , то полегшується знаходження DQ тим, що можна скористатися граничним законом Дебая, згідно з яким теплоємність пропорційна кубу термодинамічної температури,

С_m = 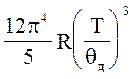                  (4)

Підставляємо молярну теплоємність (4) у формулу (3) і маємо

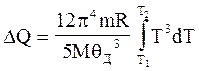
Виконаємо інтегрування

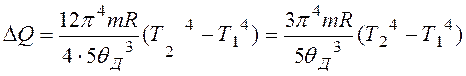
Зробимо обчислення:

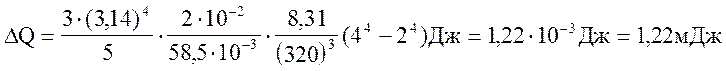
          Приклад 7. Обчислити дефект маси та енергію зв’язку ядра   ₃⁷Li.

                                                  Розв’язання