Фізика атомів і молекул. Основи квантової механіки. Фізика твердого тіла. Ядерна фізика та елементарні частинки, страница 3

          Маса ядра завжди менша суми має вільних протонів та нейтронів, з яких ядро утворилося. Дефект маси ядра  Dm - є різниця між сумою мас вільних нуклонів (протонів та нейтронів) та масою ядра

Dm = Zm_p + (A - Z) m_n - m_я ,                                    (1)

де Z - атомний номер ( число протонів ядра);

          А - масове число (число нуклонів, що складають ядро);

          m_p,    m_n, m_Я - маси протона, нейтрона та ядра.

          У таблицях додатків завжди даються маси нейтральних атомів, а не ядер, тому формулу (1) необхідно перетворити так, щоб в неї входила маса m_a  нейтрального атома, Потрібно враховувати, що маса нейтрального атома порівнюється з сумою мас ядра та електронів, що утворюють єлектронну оболонку атома,

  m_a =m_я + Zm_e

Звідси   m_Я = m_a -Zm_e                                                                    (2)

         Виразимо у рівнянні (1) масу ядра по формулі (2), маємо:

Dm =Zm_p + (A - Z)m_n - m_a + Zm_e  або Dm = Z(m_p -m_e) + ( A - Z) m_n -m_a

Помітивши, що  m_p+ m_e = m_H,

де m_H –маса атома водню, остаточно знаходимо:

          Dm = Zm_н + (А - Z)m_n - m_a       (3)

Підставимо у співвідношення (3)  числові значення мас ( по табл), маємо

Dm = [3 . 1,00783 + (7 - 3) . 1,00867 - 7 . 0,1601 ]  а.о.м. = 0,04216 а.о.м.

У відповідності з законом пропорціональності маси та енергії

Е = D m  . с² ,                        (3)

де  с - швидкість світла у вакуумі.

Коефіцієнт пропорціональності  с² можна виразити:

с² = 9 . 10¹⁶м²/с²     або с²  ≤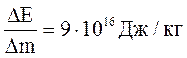

Коли обчислити енергію зв’язку, користуючись позасистемними одиницями, то  с² = 931 МеВ/а.о.м. Якщо врахувати це, то формула (3) буде мати вигляд

Е = 931 Dm (МеВ)                      (4)

Підставивши знайдене значення дефекту маси ядра у формулу (4), одержимо:                                                                                                                          Е = 931 . 0,04216 МеВ = 39,2 МеВ

          Примітка: Термін «дефект маси» вживається у другому значенні: дефектом маси  D називається різниця між масою нейтрального атома даного ізотопа та його масовим числом А:

D = m_а - А

Ця величина особливого фізичного значення не має, але її використування дозволяє у ряді випадків значно спростити обчислення.

          У данному посібнику всюди мається на увазі дефект маси Dm, який обчислюється  по формулі (1).

          Приклад 8. Знайти початкову активність А_о радіоактивного препарату магнію²⁷₁₂ Mq масою   m = 0,2 нкг та його активність  А через t = 6 год. Період піврозпаду Т _1/2 магнію рахувати відомим.

                                                  Розв’язання

          Активність  А  ізотопу характеризує швидкість радіоактивного розпаду та знаходиться відношенням числа  dN ядер, що розпалися за інтервал часу  dt, до цього інтервалу:

А ≤ -                               (1)

          Знак «-» показує , що число N радіоактивних ядер зменшується.

Для того, щоб знайти   скористуємося законом радіоактивного розпаду

N = N_oe^-lt,                      (2)

де   N -  число радіоактивних ядер ізотопа в момент часу t;

      N_o - число радіоактивних ядер у момент часу, прийнятий за початковий       (t = 0);

          l -  стала радіаційного розпаду.

Продиференцюємо співвідношення (2) за часом

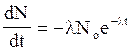                (3)

Виключивши з формул (1) та (3)  , знаходимо активність препарату в момент часу  t

 А = lN_oe^-lt                          (4)

Початкову активність А_о препарату будемо мати при  t = 0

А_о =lN_o

Стала радіоактивного розпаду   l  зв’язана з періодом піврозпаду Т_1./2 співвідношенням

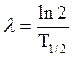                  (6)

Число N_о радіоактивних ядер ізотопа дорівнює добутку сталої Авогадро  N_A  на кількість речовини n даного ізотопа

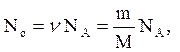               (7)

де      m - маса ізотопа;

          М - молярна маса

Враховуючи співвідношення (6)  та (7), формули (5) та (4) мають вигляд

А_о =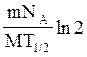              (8)

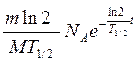А=          (9)

Зробимо обчислення, враховуючи, що Т_1/2 = 10 хв  =  600 с;

ln2 = 0,693 ;   t = 6 год = 6 . 3,6 . 10³с = 21,6 . 10³ с;

А_о =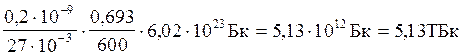

А =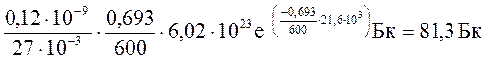

Контрольна робота 4

601. Незбуджений атом водню поглинає квант випромінювання з довжиною хвилі  l = 102,6 нм. Обчислити радіус r електронної орбіти збудженого атома водню, користуючись теорією Бора.

602. Обчислити по теорії Бора радіус r₂ другої стаціонарної орбіти та швидкість V₂ електрона на цій орбіті для атома водню.

603. Обчислити по теорії Бора період Т обертання електрона в атомі водню, який знаходиться у збудженому стані з квантовим числом n = 2.

604. Знайти максимальну енергію  e_max  серії Бальмера у спектрі випромінювання атомарного водню.

605. Знайти перший потенціал  j₁ збудження та енергію іонізації Е_і атома водню, який знаходиться у основному стані.

606. Знайти енергію e фотона, яку випромінює атом водню, коли електрон переходить з третьої орбіти на другу.

607. Знайти найбільшу   l_max та найменшу   l_min довжини хвиль в ультрафіолетовій серії водню (серія Лаймана).

608. У однозарядному іоні гелію електрон перейшов з третього енергетичного рівня на перший. Знайти довжину хвилі  l  випромінювання.

609. Електрон в атомі знаходиться на третьому енергетичному рівні. Знайти кінетичну Т, потенціальну  П та повну енергію Е електрона. Відповідь записати у електрон-вольтах.

610. Фотон вибиває з атома водню, який знаходиться у основному стані, електрон з кінетичною енергією Т = 10 еВ. Обчислити енергію  e фотона.

611. Обчислити довжину хвилі  l де Бройля для частинки масою  m = 1 г, що рухається зі швидкістю V = 10 м/с. Чи необхідно враховувати в цьому випадку хвильові властивості частинки?