Методичні вказівки до виконання контрольних робіт з курсу “Вищої математики”. Частина третя, страница 7

Варіант 25

У партії з 6 деталей 4 - стандартні. Навмання відібрано дві деталі. Скласти закон розподілу випадкової величини X - числа стандартних деталей серед двох відібраних. Знайти математичне сподівання та дисперсію цієї випадкової величини

ЗАВДАННЯ № 3.2

Дискретна випадкова величина  може приймати лише два значення:  та , причому . Відомі ймовірність  можливого значення , математичне споживання  та дисперсія . Знайти закон розподілу випадкової величини.

Варіант
1	0,5	3,5	0,25
2	0,5	3	4
3	0,1	1,9	0,09
4	0,2	2,6	0,64
5	0,5	5,5	0,25
6	0,2	1,8	0,16
7	0,2	2,8	0,16
8	0,1	2,8	0,36
9	0,4	2,2	0,96
10	0,5	2,5	2,25
11	0,9	1,4	1,44
12	0,9	1,1	0,09
13	0,9	1,2	0,36
14	0,9	1,3	0,81
15	0,8	1,2	0,16
16	0,8	1,4	0,64
17	0,8	1,6	1,44
18	0,8	1,8	2,56
19	0,8	2	4
20	0,6	1,4	0,24
21	0,6	1,8	0,96
22	0,6	2,2	2,16
23	0,6	2,6	3,84
24	0,5	1,5	0,25
25	0,5	2	1

ЗАВДАННЯ № 4

НЕПЕРЕРВНІ ВИПАДКОВІ ВЕЛИЧИНИ

Випадкову величину задано функцією . Знайти:

а)  щільність розподілу ймовірностей, математичне сподівання та дисперсію випадковою величини;

б)  ймовірність того, що в результаті випробування випадкова величина прийме значення, яке належить інтервалу .

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 

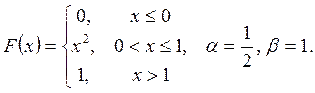
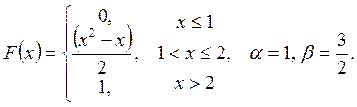
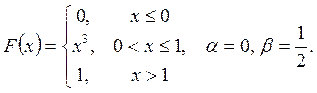
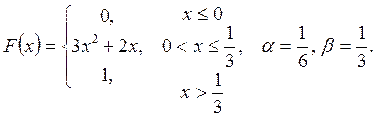
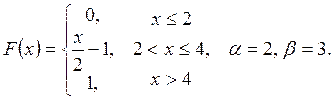
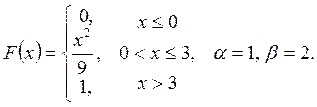
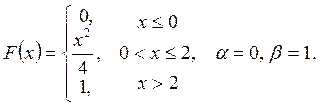
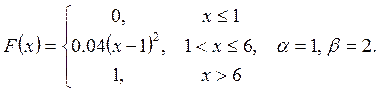
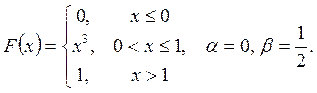
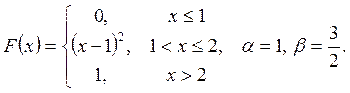
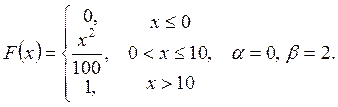
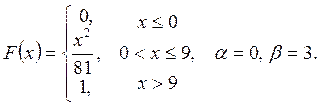
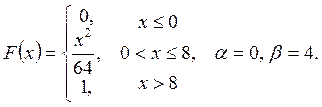
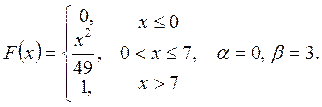
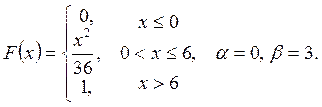
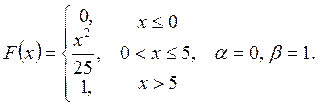
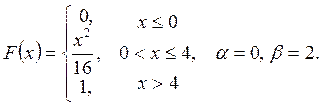
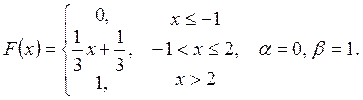
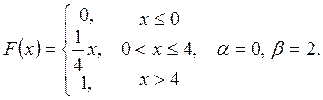
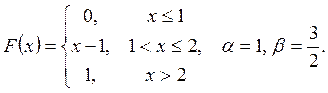
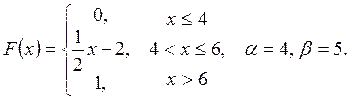
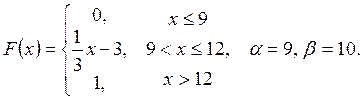
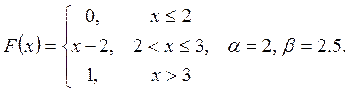
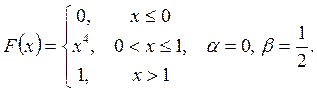
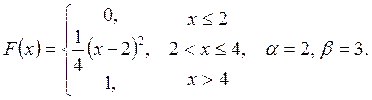
ЗАВДАННЯ № 5

НОРМАЛЬНИЙ РОЗПОДІЛ

Відомі математичне сподівання  та середнє квадратичне відхилення  нормально розподіленої величини . Знайти:

1.  ймовірність того, що в результаті випробування випадкова величина попадає в інтервал ;

2.  ймовірність того, що абсолютна величина відхилення випадкової величина від свого математичного сподівання менша за додатне число .

Варіант						Варіант
1	13	7	8	11	2	14	7	2	3	10	1
2	12	3	7	13	5	15	6	3	2	11	5
3	9	5	3	10	6	16	5	4	2	12	3
4	8	9	10	16	10	17	4	5	2	11	7
5	14	8	4	18	8	18	3	2	3	6	3
6	3	10	5	12	16	19	2	5	4	9	9
7	7	10	14	19	12	20	2	4	6	10	5
8	5	6	12	16	12	21	15	2	12	19	3
9	4	11	16	23	24	22	14	4	10	20	8
10	6	13	15	26	8	23	13	5	11	21	8
11	10	4	2	13	6	24	12	5	12	22	12
12	9	5	5	14	6	25	11	8	13	23	6
13	8	2	4	9	3

СПІСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ.

1.  Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. 4. 2 - М.: Высшая школа, 1986. -415 с.

2.  Павленко Т.В. Самостійно вивчаемо курс теорії ймовірностей і математичної статистики. Ч.1. Теорія ймовірностей: Навч.посібн.-Алчевськ: ДонГТУ, 2005.-126с.

3.  Манаков В.П., Різун В.І. Теорія ймовірностей та математична статистика для економічних спеціальностей. Навч.посібн.- Алчевськ: ДГМИ, 2000.-284с.

4.  Пак В. В., Носенко Ю. Л. Высшая математика. Учебник - Д.: Сталкер, 1997. - 560 с.

5.  Пискунов Н. С. Дифференциальное и интегральное исчисления. - М.: Высшая школа, 1976. - Т. 2. -576 с.

6.  Подлипенська Л.Є. Математична статистика для гірняків: Навч.посібн.-Алчевськ: ДГМИ, 2004.-171с.

Варіанти завданнь: