Методические указания к лабораторным работам по курсу "Автоматизация конструкторского и технологического проектирования РЭС", страница 3

Выходные параметры: В – массив из действительных чисел (он же входной) при выходе из программы содержит решение системы, если KS = 0, то в массиве В содержится решение системы, если KS = I, исходная система не имеет единственного решения (определитель системы равен 0).

Перед обращением к подпрограмме SIMQ необходимо:

1. Описать массивы А и В. Если система содержит n-уравнений, то массив А должен содержать n*n элементов, а массив В - n элементов.

2. Присвоить элементам массивов А и В значения коэффициентов системы следующим образом:

А(1) = а₁₁, А(2) = а₂₁, ... . А(N) = a_n, A(N+1) = a12, A(N*N) = a_nn, B(1) = b₁, B(2) = b₂, ... . B(N) = b_n.

3. Присвоить значение параметру N, который равен числу уравнений системы.

4. Проверить соответствие фактических параметров по типу и порядку следования формальным параметрам подпрограммы SIMQ. Параметры А и В – величины вещественного типа, N и КS – целого типа.

3. Приближённое вычисление интеграла методом Симпсона.

Для приближённого вычисления интеграла чаще всего подынтегральную функцию заменяют "близкой" ей вспомогательной функции. В частности, если при вычислении 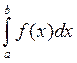 подынтегральную функцию f(x) заменить интерполяционным многочленом второй степени, достроенным по значениям функции в трёх точках а, (а + в)/2, в , то получатся так называемая простая квадратурная формула Симпсона

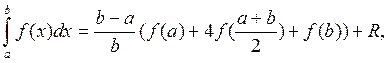
где R – остаточный член. Если f ⁴(x) непрерывна на 1а, в1, то

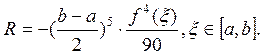
Для повышения точности интегрирования применяют составную формулу Симпсона:

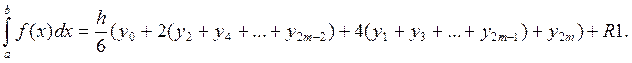
Для приближенного вычисления интеграла 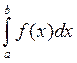 по составной Формуле Симпсона предназначена подпрограмма (SUBROUTINE) SIMPS (A, B, N, F, Y).

SUBROUTINE SIMPS(A,B,N,F,Y)

H=(B-A)/N

Y=0

X=A

DO 1 I=2,N

Y(I)=Y(I)+F(x)+4*F(x+H)+f(x+2*H)

1    x=x+2*H

y=Y*H/3

RETURN

END

Входные параметры: А – нижний предел интегрирования; В – верхний предел интегрирования,

N – целее чётное число отрезков, на которые разбивается промежуток интегрирования, F – имя внешней подпрограммы, вычисляющей значения подынтегральной функции.

Выходные параметры: Y – приближённое значение интеграла.

Перед обращением к подпрограмме SIMPS необходимо:

1. Составить подпрограмму – функцию F(x), вычисляющую значения подынтегральной функции, имя подпрограммы F должно быть переменной действительного типа.

2. Описать имя Р в головной программе оператором 'EXTERNAL.

3. Присвоить в головной программе значения переменным А, В, N. При этом необходимо проверить, соответствуют ли фактические параметры по типу и порядку следования формальным параметрам программы.

Как правило, РЭА представляет собой комплекс конструктивных модулей, объединённых механическими, электрическими и иными связями и выполняющих заданные функции в соответствии с целевым назначением. РЭА можно представить как многоуровневую иерархическую структуру, состоящую из пяти уровней:

– уровень 0 образует неделимые составляющие, такие как; радиоэлементы и микросхемы БИС, СБИС);  

– уровень I включает микросборки, микромодули и другие объёмные; базовые модули;      

– уровень 2 объединяем сборочные, единицы или ячейки (обычно собранные на базе печатных плат);

– уровень 3 включает блоки и конструктивно законченные сборочные единицы;

– уровень 4 образует аппаратура, т.о. функционально и конструктивно законченное изделие электронной техники.

В качестве изделия электронной техники может быть составляющая любого из перечисленных уровней.sto и операционный усилитель (ОУ) выполненный в виде интегральной схемы и однокристальная ЭВМ и магнитофон для записи, и система слежения за, спутником.

На уровне 0 в качестве примеров математических моделей ИЭТ рассмотрим модели сопротивления, источников напряжения и тока, ёмкости и индуктивности.

МОДЕЛЬ СОПРОТИВЛЕНИЯ. Пусть имеется электрическая цепь (рис.5.2.) с последовательно соединенными сопротивлениями R и генератором тока I. В цепь включены амперметр и вольтметр для измерения соответственно тока i в цепи и падения напряжения U на сопротивлении.