Методические указания к лабораторным работам по курсу "Автоматизация конструкторского и технологического проектирования РЭС", страница 2

Объект моделирования	Электрическая система
Рассеиватель энергии	Резистор
Модель	Сопротивление
Накопитель электрической энергии	Конденсатор (электрический)
Модель	Ёмкость (электрическая)
Накопитель магнитной энергии	Катушка индуктивности
Модель	Индуктивность

Описание математических методов

 Решение задачи Коши методом дилера. Пусть требуется найти приближённое решение диф, уравнения y’= f(x,y) удовлетворяющее данному условию y(x0) = y0. Численное решение задачи состоит в построении таблицы приближённых значений y1, y2, …, yn,  решения уравнения y(х) в точках х1, х2, x3, ..., хn. Чаще всего xi = x0 + ih, i = 1,2,... , n. Точки xi  называются узлами сетки, а величина h - шагом (h>0). В методе Эйлера величины yi вычисляются по формуле    

Yi+1 = yi + hf(xi, yi),     i = 0,1,2, …                     (1)

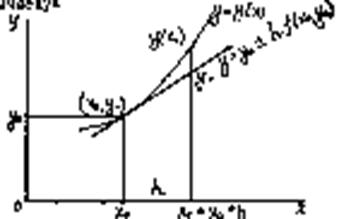Этот метод относится к группе одношаговых методов, в которых для расчёта точки (xi+1, yi+1) требуется информация только о последней вычисленной точке (xi, yi). Метод допускает простую геометрическую интерпретацию.

Предположим, что известна точка (xi, yi); определяется уравнением касательная к этой кривое проходящая через точку y = yi + y’i (x - xi), а так как y’i = f(xi, yi) и xi+1 = xi + h, то yi+1 = yi + hf(xi, yi). Для оценки погрешности метода на одном шаге сетки разложим точное решение в ряд Тейлора в окрестности узла xi.

Y(xi+1) = y(xi + h) = y(xi) + y’(xi)h + 0(h*h) = y(xi) + hf(xi, yi) + 0 (h*h)     (2)

Сравним (I) и (2). Сравнение показывает, что они согласуются до членов первого порядка по h, а погрешность формулы (1) равно 0(h²). Если расчётные формулы численного метода согласуются в ряд Тейлора до членов порядка h, то число р называют порядком метода. Т.о. метод Эйлера - метод первого порядка.

Метод Эйлера легко обобщается на случай нормальных систем диф. уравнений. Пусть требуется найти решение системы диф. уравнений.

y’i = f1(x, y1, …, yn),

………………………

…

y’n = fn(x, y1, …, yn),

удовлетворяющих начальным условиям y1(x0) = y10, y2(x0) = y20, …, yn(x0) = yn0   или в векторной форме    Y’ = f(x, Y), Y(x0) = Y0.

Y(x) = {y1(x), y2(x), …, yn(x)}, Y0 = {y10, y20, …, yn0}.

Входные параметры: N – порядок системы, Х - начальное значение Хо, Y – массив из N чисел, содержащий начальное значение у; Н - значение шага; Р - имя внешнем подпрограммы SUBROUTINE P(x, y, f), вычисляющей значения правых частей уравнений системы по заданным Х и Y и размещающий их в элементах. массива F: F - рабочий массив размерности содержащий  значения f(X,У).

Выходные параметры: Х – значение x0 + h, Y – массив из М чисел, содержащий приближённое решение в точке x0 + h.

(Y(I) = Y1 = yi(x0 + h), I = 1, 2, …, N )

Перед обращением к подпрограмме EYLER необходимо:

- составить подпрограмму P(X, Y, F) вычисления правых частей  уравнений системы;

- описать имя Р оператором EXTERNAL;

- описать размерность массивов Y и F;

присвоить фактические значения параметрам N, Х, Y, Н. Следует пометь, что входные параметры Х и Y являются одновременно и выходными.

Листинг программы дан в приложении I.

2. Метод Гаусса для решения системы линейных уравнений, Методом Гаусса называют точный метод решения невырожденной системы линейных уравнений, состоящий в том, что последовательным исключением неизвестных систем

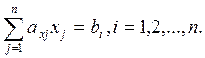
приводят к эквивалентной системе с треугольной матрицей

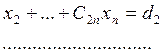
решение которой находят по рекуррентным формулам

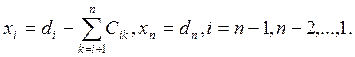
Один из алгоритмов описан в подпрограмме SUBROUTINE SIMQ (A, B, N, KS).

Текст подпрограммы дан в приложении 3.

Входные параметры: N – целое положительное  число, равное порядку n системы; А – массив из N*N действительных чисел, содержащий матрицу коэффициентов системы А(1) = а11, А(2) = а21, ... . А(N) = a_n, A(N+1) = a12, A(N*N) = a_nn; В – массив из   действительных чисел, содержащий столбец свободных членив системы B(1) = b1, B(2) = b2, ... . B(N) = b_n.