Информатика и выч. техника \ Автоматизация конструкторского и технологического проектирования РЭС

Методические указания к лабораторным работам по курсу "Автоматизация конструкторского и технологического проектирования РЭС", страница 10

Информация о первоначальном размещении элементов по посадочным ютам платы задаётся вектором-строкой размещения Р1*n, элемент которой Рk = j показывает, что на  j- м посадочном месте размещён элемент с номером К. Для варианта размещения, приведённого на рис.2, вектор размещения имеет вид:

i1

2

3

4

5

6

7

8

9

10

M11

2

8

5

12

1

9

3

6

4

                                                                 

Вектор Р является как входным, так и выходным. Иногда конструктору греется зацепить некоторые элементы на исход л варианте размещения. Для этого служит вектор-строка Z1*n, элемент который равен 1, если к-й элемент закреплён на посадочном месте, указанном в Р. Если к-й элемент не закреплён и может участвовать в перестановках, то Zk = 0.

Оптимизация размещения методом парных перестановок заключается в следующем.

Шаг I. На первоначальном этапе размещения (который задаётся конструктором или находится с помощью одного из последовательных алгоритмов) производятся очередная парная перестановка модуля   с модулем. Эти модуля не должны быть помечены как закреплённые. Количество таких неповторяющихся перестановок, которые можно выполнить на начальном варианте размещения модулей, равно

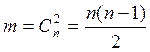                                            (3)

Шаг 2. После каждой перестановки подсчитывается приращение целевой функции. Приращение суммарной длины сигнальных связен, возникающее в результате перестановки модуля    с модулем, вычисляется по формуле:       

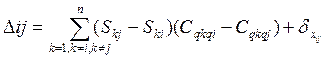         (4)

Величина  равна приращению длины сигнальных связей, соединяет переставляемые элементы с электрическим соединителем.

Шаг 3. После всех возможных перестановок определяется пара модулей; перестановка которых приводит к наибольшему улучшению целевой функции. Математически эта перестановка должна удовлетворять следующему условию:  

Шаг 4. В результате выполнения этой перестановки образуется новый улучшенный вариант размещения, принимаемый за начальный. Информация в массиве С изменяется и выполняется следующая итерация (переход к шагу 1.)

Шаг 5. Алгоритм заканчивает свою работу в случаях: а) если исчерпано заданное число итераций;

б) если на очередной итерации достигнута заданная точность решения ;

в) если на очередной итерации ни одна из возможных парных перестановках не приведёт к улучшению целевой функции, т.е.

                         (5)

Точность решета задачи размещения модулей значительно возрастает при использовании в качества целевой функции суммарной длины минимальных деревьев, построенных на контактах каждой цепи.

При этом возрастает время решения задачи и требуется ЭВМ с высоким быстродействием.

Порядок выполнения работы.

I. Утвердить у преподавателя эскиз платы.

И. Изучить теоретическую часть.

3. Изучить программу выполнения итерационного алгоритма.

5. Рассчитать задачу на ЭВМ. Текст программы хранится в каталоге KIPPA.

6. Составить отчёт с полученным машинным вариантом размещения. Сделать выводы по полученным результатам.

Текст программы дан в приложении.            

Используемая литература.

1. Норенков И.П. Введение в автоматизированное проектирование "

технических устройств и систем, М, Высшая школа,1980.

2. Норенков И.П., Манячев В.Б. Системы автоматизированного проектирования вычислительной аппаратурв. М., Высшая школа, 1986 г.

Лабораторная работа № 5.

ИССЛЕДОВАНИЕ НАДЁЖНОСТИ БЛОКА РЭА И РАСЧЁТ ТЕПЛОВОГО  РЕЖИМА БЛОКА.

Цель работы: Изучить расчёт на надёжность. Сделать соответствующий расчет на ЭВМ.

Выполнить тепловой расчёт данного блока.

Исследование надёжности блока РЭА является заключительным этапом при проектировании узлов и блоков РЭА.

Требования к надёжности на изделия конкретного вида указываются в соответствии с ГОСТ 20397-82.

Скачать файл