Операторные схемы составляются на основе компонентных уравнений в операторной форме, составленные после коммутации.
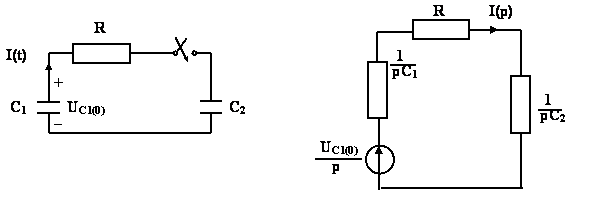 Пример:
Пример:
Теорема разложения применяется для перехода от операторного изображения к оригинальному.
![]()
F2(p) = 0 Þ P1 ,P2 ,… Pn , тогда
![]() , откуда
, откуда
![]() ,
,
где
![]()
Замечание: порядок числителя должен быть меньше порядка знаменателя.
Пример: Записать оригинал
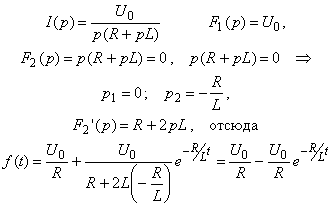
Для аналитической записи импульсных воздействий применяются единичная ступенчатая функция (функция Хевисайда) и запаздывающая функция Хевисайда.
 1(t) = 1 (t > 0)
1(t) = 1 (t > 0)
1(t) = 0 (t< 0)
1(t – t1) = 1 (t > t1)
1(t – t1) = 0 (t < t1)

|
![]() 1)
1)
 |
|||
![]()
 2)
2)
![]()
 3)
3)
![]()
Чтобы представить полученные аналитические выражения в операторной форме, найдем изображение запаздывающей функции:
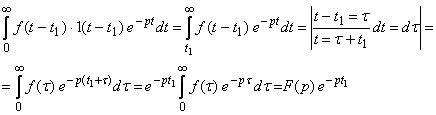
Используя полученную функцию изобразим 1 ¸ 3 в операторной форме:
1) ![]() ;
;
2) ![]() ;
;
3) ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.