Теорема разложения. Расчет переходных процессов при импульсных воздействиях. Операторные и временные характеристики электрических цепей, страница 2

Операторной характеристикой электрической цепи называется:

,

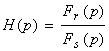где F_r(p) – реакция цепи на сигнал F_s(p).

Если известна операторная характеристика цепи, то:

1.  F_s(p) ¸ f_s(t);

2.  F_r(p) = H(p) ^. F_s(p);

3.  f_r(t) ¸ F_r(p).

операторная характеристика содержит в себе полную информацию о цепи.

Пример:

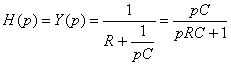
Определить ток, если f_s(t) = U(t) = U₀ .

                         1.  ;

                         2.  ;

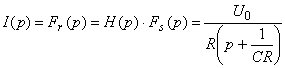                         3.  .

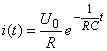Оригинал H (p) называется импульсной характеристикой (h(t)).

Оригинал  называется переходной функцией (h₁(t)).

Частотной характеристикой цепи называется .

,

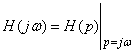где H(w) – амплитудо-частотная характеристика,

      Y(w) – фазо-частотная характеристика.

Лекция 6

1.8.  Интеграл свертки

С помощью интеграла свертки по известной импульсной характеристике цепи можно определить реакцию цепи на любой сигнал.

1.9.  Интеграл Дюанеля

С помощью интеграла Дюанеля по известной переходной характеристике цепи можно определить реакцию цепи на любой сигнал.

1.10.  Спектральный метод исследований переходных процессов

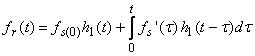
В основу спектрального метода положено преобразование Фурье.

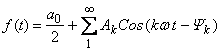
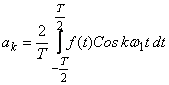                                             (1)   

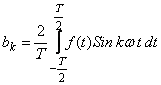                                              (2)

,

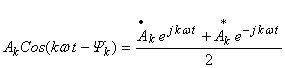где              

С учетом формулы Эйлера ряд Фурье можно представить в виде:

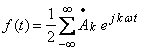                                                 (3)

Домножим (2) на j и вычтем из (1)

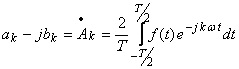
Ряд Фурье применим только для периодических функций с периодом .

Распространим ряд Фурье на случай непериодических функций: T = ¥,

;

таким образом  , тогда

.

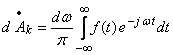Спектральной плотностью назовем:

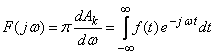 – прямое преобразование Фурье.

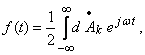
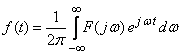 – обратное преобразование Фурье.

С помощью преобразований Фурье для любой реальной функции можно найти ее спектральную плотность (Спектр) и наоборот.