Теорема разложения. Расчет переходных процессов при импульсных воздействиях. Операторные и временные характеристики электрических цепей, страница 3

Для функций, заданных только справа от нуля (f (t) ^. 1 (t)), прямое преобразование Фурье приобретает вид:

.

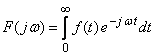Пример: Найти спектральную плотность:

 

                                                                                        

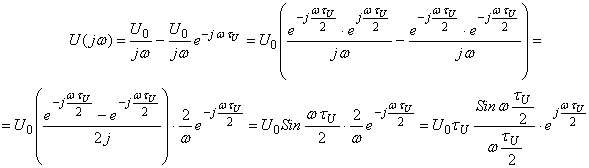
Из полученного:

                 АЧХ      ;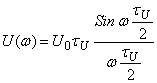

                 ФЧХ      .

1.11.  Передача сигналов через четырехполюсники

1.  Идеальная неискажающая система имеет частотную характеристику:

.

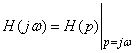Условие неискажения:

, тогда

                                                  , следовательно

 – операторная характеристика неискажающей системы;

– частотная характеристика неискажающей системы.

АЧХ  –  H (w) = a

ФЧХ  –  Y (w) = – t₁w

2.  Идеальные дифференцирующие системы

;

              АЧХ – H (w) = aw

              ФЧХ – Y (w) =

Реальная дифференцирующая цепь образуется следующим образом:

 

                                                                                                     f_r (t) = U₂ (t),

                                                                                                     f_s (t) = U₁ (t).

.

.

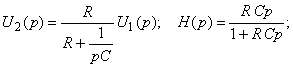
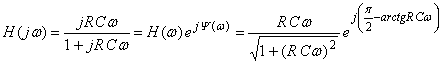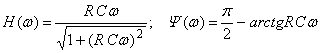Для дифференцирования необходимо выполнение условия:

RCw <<< 1 или w <<< .

Лекция 7

3.  Идеальное интегрирующее звено:

,

.

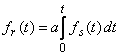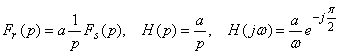Реальная интегрирующая цепь образуется следующим образом:

 

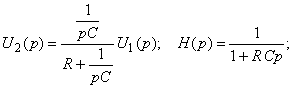
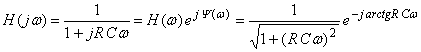
Для интегрирования необходимо:

RCw >>> 1 или w >>> .