Теорема разложения. Расчет переходных процессов при импульсных воздействиях. Операторные и временные характеристики электрических цепей, страница 4

1.12.  Обратная связь

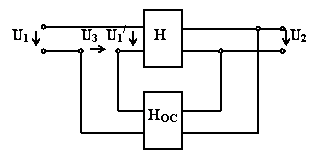
Вреальных устройствах характеристики отличаются от идеальных. Для коррекции частотных характеристик применяют обратные связи.

 

                                                                                             

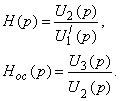
Таким образом обратная связь может корректировать передаточную         функцию H(p).

1.13.  Синтез цепей

Синтезом линейной электрической цепи называют определение структуры цепи и числовых значений составляющих ее элементов R, L, C по известным операторным выражениям этой цепи или по временным характеристикам при воздействии на выход импульса определенной формы.

Если представить входное сопротивление двухполюсника в виде

,

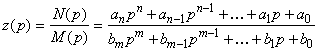то должны выполняться следующие пять условий:

1.  все коэффициенты a и b должны быть неотрицательны;

2.  наивысшая степень полинома числителя (n) не может отличаться от наивысшей степени полинома знаменателя (m) более чем на 1;

3.  если условиться значения p, при которых z (p) = 0, называть нулями функции z (p), а значения p, при которых z (p) = ¥, называть полюсами, то нули и полюсы должны быть расположены только в левой части плоскости p;

4.  нули, расположенные на мнимой оси плоскости p, должны быть только простые, не кратные;

5.  если вместо p в выражение z (p) подставить jw, то при любом значении w должно быть Re z (jw) ³ 0.

Лекция 8

1.13.1.    Метод Бруне

1.  Проверка – не содержит-ли z_зад(p) полюсов на мнимой оси. Если они имеются, то из состава z_зад(p) выделяют, соответствующие им последовательно включенные параллельные резонансные контуры:

.

2.  Полагая p = jw, находят Re z (jw) и определяют w, при которой Re z (jw) минимальна (R_min).

3.  Из z (p) вычитают R_min и находят z₁(p).

4.  если частота, при которой имеет место минимум Re z (jw), равна нулю или бесконечности, то уже на этой стадии делается попытка реализовать z (p) лестничной схемой, если нет, то:

5.  Определяют z₁(p) при p = jw₀.

6.  Возможны два случая. Первый, когда x₁ > 0, второй, когда x₁ < 0. Будем полагать, что x₁ = w₀ L₁ > 0, тогда

.

7.  Составляется разность z₁(p) –­ pL₁ и приводится к общему знаменателю.

8.  Поскольку p = jw₀  z₁(p) –­ pL₁ = 0, то Y₀ (p) = ¥, то есть p = jw₀ является полюсом Y₀ (p). Наличие полюса у Y₀ (p) позволяет представить оставшуюся часть двухполюсника ветвью из последовательно соединенных L₂ и C₂ настроенной в резонанс на частоту w₀ и параллельно ей присоединенного двухполюсника с сопротивлением z₂ (p):