ЛАБОРАТОРНАЯ РАБОТА № 79
ИССЛЕДОВАНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ
Цель работы: Измерить зависимость амплитуд напряжения на конденсаторе и силы тока в контуре от частоты внешнего напряжения; определить резонансные характеристики контура.
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
|
Рис 1. Схема для изучения вынужденных колебаний |
Чтобы вызвать вынужденные электрические колебания надо последовательно с элементами контура, состоящего из катушки индуктивности L, конденсатора емкостью C и активного сопротивления R, включить переменную э. д. с. или, разорвав контур, подать на образовавшиеся контакты переменное напряжение (рис. 1).
Uвнеш = U0cos(wt), (1)
где U0 – амплитуда (максимальное значение) внешнего напряжения.
Условимся считать положительным ток, заряжающий конденсатор (левую обкладку на рис. 1). Тогда сила переменного тока
![]() , (2)
, (2)
где q – заряд левой обкладки конденсатора.
Для цепи запишем закон Ома
JR = j1 – j2 + es + Uвнеш, (3)
где j1 – j2 = –U = –![]() – напряжение на конденсаторе, es =
– напряжение на конденсаторе, es = ![]() – э. д. с. самоиндукции в катушке.
С учетом этих соотношений и после подстановки (1) в (2) из уравнения (3)
получим неоднородное линейное дифференциальное уравнение второго порядка
относительно величины q,
которое называется дифференциальным уравнением вынужденных колебаний:
– э. д. с. самоиндукции в катушке.
С учетом этих соотношений и после подстановки (1) в (2) из уравнения (3)
получим неоднородное линейное дифференциальное уравнение второго порядка
относительно величины q,
которое называется дифференциальным уравнением вынужденных колебаний:
![]() , (4)
, (4)
где b – коэффициент затухания; w0 – собственная частота колебаний в контуре (частота свободных незатухающих колебаний в контуре с R = 0). Для колебательного контура
![]() ,
, ![]() , (5)
, (5)
Для практических целей удобнее рассматривать в качестве переменной величины не заряд, а напряжение на конденсаторе U. Тогда из (4) будем иметь
![]() . (6)
. (6)
Это уравнение отличается от дифференциального уравнения свободных затухающих колебаний только наличием ненулевой правой части, поэтому его общее решение будет иметь вид суммы общего решения уравнения затухающих колебаний и частного решения уравнения (6). При этом первое слагаемое с течением времени становится пренебрежимо мало, а второе слагаемое, которое называют уравнением вынужденных установившихся колебаний, не зависит от начальных условий. Будем искать это частное решение в виде
U = Umcos(wt – y). (7)
|
Рис. 2. Вращающийся вектор в методе век- торных диаграмм |
Для определения амплитуды Um и фазы y (так называют разность фаз между
внешним воздействием и смещением) вынужденных колебаний воспользуемся методом
векторных диаграмм. В его основе лежит взаимно однозначное соответствие между
процессом колебаний, описываемым уравнением x = Acos(wt + j) и проекцией на ось х
вращающегося против часовой стрелки вектора ![]() длиной А
с угловой скоростью w, который в начальный момент времени расположен под углом j к оси х (рис. 2).
длиной А
с угловой скоростью w, который в начальный момент времени расположен под углом j к оси х (рис. 2).
С помощью правил дифференцирования тригонометрических функций представим все слагаемые в левой части (6) в одинаковом функциональном виде (отличие будет только в амплитудах и начальных фазах). Из (7) следует
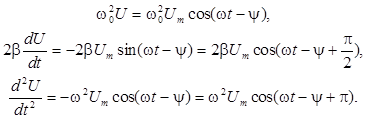
|
Рис. 3. Применение метода векторных диаграмм к дифференциальному уравнению вынужденных колебаний |
В соответствии с методом векторных
диаграмм эти три слагаемые соответствуют векторам с длинами ![]() , 2bwUm,
, 2bwUm, ![]() и расположенных (в начальный момент
времени) под углами –y,
и расположенных (в начальный момент
времени) под углами –y, ![]() , p – y к оси х. В соответствии с
(6) их сумма равна вектору с длиной
, p – y к оси х. В соответствии с
(6) их сумма равна вектору с длиной ![]() , который
расположен параллельно оси х. На рис. 3 представлены все три вектора и
их сумма. По теореме Пифагора
, который
расположен параллельно оси х. На рис. 3 представлены все три вектора и
их сумма. По теореме Пифагора
![]() .
.
Из этого соотношения и из треугольника ОАВ следуют соотношения для амплитуды и фазы вынужденных колебаний
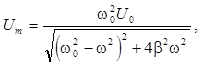 (8а)
(8а)
![]() (8б)
(8б)
В правильности полученных соотношений можно убедиться прямой подстановкой (7) с учетом (8а) и (8б) в (6).
Амплитуда вынужденных колебаний немонотонно зависит от частоты внешнего напряжения w. Она имеет локальные минимумы при w = 0 (Um0 = U0) и при w ® ¥ (Um¥ ® 0), а также максимум, для определения положения которого достаточно методами математического анализа найти значение w (wр), при котором подкоренное выражение в знаменателе правой части уравнения (8а) имеет минимум. После простых расчетов получим
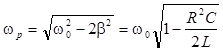 . (9)
. (9)
Последнее равенство в (9) верно для колебательного контура.
В практически важном случае, когда затухание мало (b << w0) имеем wр w0.
Для колебательного контура после подстановки (5) из (8а, б) получим
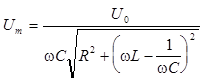 , (10а)
, (10а)
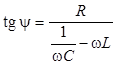 ,
(10б)
,
(10б)
Зависимость силы тока в контуре от времени следует из (2) и (7)
![]() , где Jm = wCUm – амплитуда силы тока;
, где Jm = wCUm – амплитуда силы тока; ![]() – начальная фаза силы тока. С учетом этого из (10а, б) получим
– начальная фаза силы тока. С учетом этого из (10а, б) получим
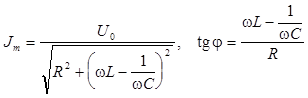 . (11)
. (11)
Из (11) следует, что Jm достигает максимального значения при w = w0 (напомним, что максимум для Um наблюдается при wр < w0).
Явление резкого возрастания амплитуды вынужденных колебаний (в нашем случае Jm и Um) при совпадении частоты внешнего периодического воздействия (w) с собственной частотой системы (w0) называется резонансом. Частоту w0 поэтому также называют резонансной частотой. Отличие wр от w0 несущественно, т. к. резкое возрастание (как будет показано дальше) возможно только в случае слабого затухания (b << w0), когда wр » w0. Найдем отставание по фазе j силы тока в контуре от напряжения внешнего источника при резонансе (т. е. при w = w0)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.